Advertisements
Advertisements
प्रश्न
ΔABP ~ ΔDEF and A(ΔABP) : A(ΔDEF) = 144:81, then AB : DE = ?
उत्तर
`("A"(Δ"ABP"))/("A"(Δ"DEF")) = 144/81` ......(i)[Given]
`("A"(Δ"ABP"))/("A"(Δ"DEF")) = "AB"^2/"DE"^2` .......(ii)[Theorem of areas of similar triangles]
∴ `"AB"^2/"DE"^2 = 144/81` .......[From (i) and (ii)]
∴ `"AB"/"DE" = 12/9` or `4/3` .......[Taking square root of both sides]
APPEARS IN
संबंधित प्रश्न
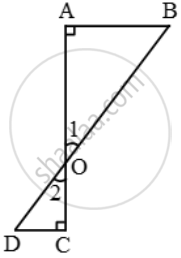
In figure, if ∠A = ∠C, then prove that ∆AOB ~ ∆COD
P and Q are points on sides AB and AC respectively of ∆ABC. If AP = 3 cm, PB = 6cm. AQ = 5 cm and QC = 10 cm, show that BC = 3PQ.
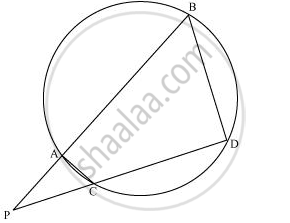
In the given figure, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC ∼ ΔPDB
(ii) PA.PB = PC.PD
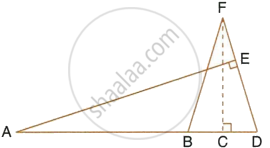
Given: FB = FD, AE ⊥ FD and FC ⊥ AD.
Prove that: `(FB)/(AD) = (BC)/(ED)`.
In triangle ABC, AD is perpendicular to side BC and AD2 = BD × DC. Show that angle BAC = 90°.
In the given figure, QR is parallel to AB and DR is parallel to AB and DR is parallel to QB.
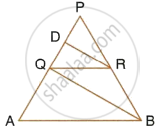
Prove that: PQ2 = PD × PA.
A line PQ is drawn parallel to the base BC of ∆ABC which meets sides AB and AC at points P and Q respectively. If AP = `1/3` PB; find the value of:
- `"Area of ΔABC"/"Area of ΔAPQ"`
- `"Area of ΔAPQ"/"Area of trapezium PBCQ"`
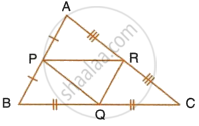
In the given triangle P, Q and R are the mid-points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.
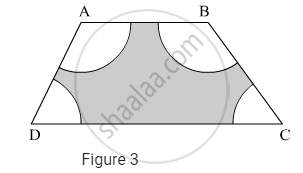
In Figure 3, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and the distance between AB and DC is 14 cm. If arcs of equal radii 7 cm have been drawn, with centres A,B, C and D, then find the area of the shaded region.
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and angle ABC = 90°.
Calculate : the area of the plot in sq. km.
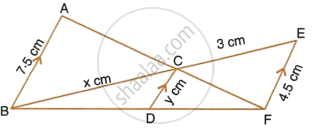
In the figure, given below, AB, CD and EF are parallel lines. Given AB = 7.5 cm, DC = y cm, EF = 4.5 cm, BC = x cm and CE = 3 cm, calculate the values of x and y.
In ΔABC, point D divides AB in the ratio 5:7, Find: BC, If DE = 2.5cm
In the given figure, PB is the bisector of ABC and ABC =ACB. Prove that:
a. BC x AP = PC x AB
b. AB:AC = BP: BC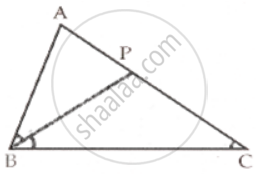
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The length of the truck
In any triangle _______ sides are opposite to equal angles
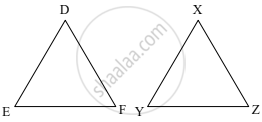
In ΔDEF and ΔXYZ, `"DE"/"XY" = "FE"/"YZ"` and ∠E ≅ ∠Y. _______ test gives similarity between ΔDEF and ΔXYZ.
In ΔABC, AP ⊥ BC and BQ ⊥ AC, B−P−C, A−Q−C, then show that ΔCPA ~ ΔCQB. If AP = 7, BQ = 8, BC = 12, then AC = ?
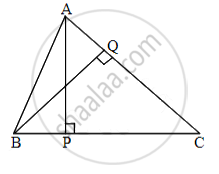
In ΔCPA and ΔCQB
∠CPA ≅ [∠ ______] ...[each 90°]
∠ACP ≅ [∠ ______] ...[common angle]
ΔCPA ~ ΔCQB ......[______ similarity test]
`"AP"/"BQ" = (["______"])/"BC"` .......[corresponding sides of similar triangles]
`7/8 = (["______"])/12`
AC × [______] = 7 × 12
AC = 10.5
In a square of side 10 cm, its diagonal = ______.
ABCD is a parallelogram. Point P divides AB in the ratio 2:3 and point Q divides DC in the ratio 4:1. Prove that OC is half of OA.

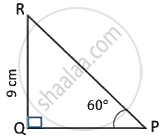
In the adjoining diagram the length of PR is ______.