Advertisements
Advertisements
प्रश्न
A line PQ is drawn parallel to the base BC of ∆ABC which meets sides AB and AC at points P and Q respectively. If AP = `1/3` PB; find the value of:
- `"Area of ΔABC"/"Area of ΔAPQ"`
- `"Area of ΔAPQ"/"Area of trapezium PBCQ"`
उत्तर
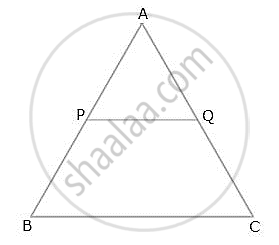
`AP = 1/3 PB => (AP)/(PB) = 1/3`
i. In ΔAPQ and ΔABC,
As PQ || BC, corresponding angles are equal
∠APQ = ∠ABC
∠AQP = ∠ACB
∆APQ ~ ∆ABC
`"Area of ΔABC"/"Area of ΔAPQ"= (AB^2)/(AP^2)`
= `4^2/1^2`
= 16 : 1
`((AP)/(PB) = 1/3 => (AB)/(AP) = 4/1)`
ii. `"Area of ΔAPQ"/"Area of trapezium PBCQ"`
= `"Area of ΔAPQ"/"Area of ΔABC – Area of ΔAPQ"`
= `1/(16 - 1)`
= `1/15`
= 1 : 15
APPEARS IN
संबंधित प्रश्न
E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR:
PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
The ratio between the corresponding sides of two similar triangles is 2 is to 5. Find the ratio between the areas of these triangles.
If in ∆DEF and ∆PQR, ∠D ≅ ∠Q, ∠R ≅ ∠E then which of the following statements is false?

A model of a ship is made with a scale factor of 1 : 500. Find
The volume of the ship, if the volume of its model is 200 cm3.
Equilateral triangles are drawn on the sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.
In the given figure ABC and CEF are two triangles where BA is parallel to CE and AF: AC = 5: 8.
(i) Prove that ΔADF ∼ ΔCEF
(ii) Find AD if CE = 6 cm
(iii) If DF is parallel to BC find area of ΔADF: area of ΔABC.
If figure OPRQ is a square and ∠MLN = 90°. Prove that ∆QMO ~ ∆RPN

ΔABC ~ ΔDEF. Write the ratios of their corresponding sides
In the figure PQ || BC. If `"PQ"/"BC" = 2/5` then `"AP"/"PB"` is ______.

In ∠BAC = 90° and AD ⊥ BC. A then ______.

