Question

A line PQ is drawn parallel to the base BC of ∆ABC which meets sides AB and AC at points P and Q respectively. If AP = `1/3` PB; find the value of:

1. `"Area of ΔABC"/"Area of ΔAPQ"`
2. `"Area of ΔAPQ"/"Area of trapezium PBCQ"`

Answer 1

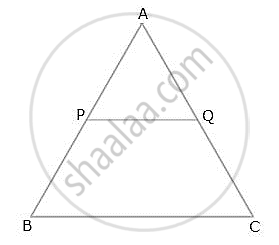
`AP = 1/3 PB => (AP)/(PB) = 1/3`

i.  In ΔAPQ and ΔABC,

As PQ || BC, corresponding angles are equal

∠APQ = ∠ABC

∠AQP = ∠ACB

∆APQ ~ ∆ABC

`"Area of ΔABC"/"Area of ΔAPQ"= (AB^2)/(AP^2)`

= `4^2/1^2`

= 16 : 1

`((AP)/(PB) = 1/3 => (AB)/(AP) = 4/1)`

ii. `"Area of ΔAPQ"/"Area of trapezium PBCQ"`

= `"Area of ΔAPQ"/"Area of ΔABC – Area of ΔAPQ"`

= `1/(16 - 1)`

= `1/15`

= 1 : 15