Question

Construct a triangle similar to a given triangle PQR with its sides equal to `2/3` of the corresponding sides of the triangle PQR (scale factor `2/3 < 1`)

Answer 1

Given ∆PQR, we are required to construct another triangle whose sides are `2/3` of the corresponding sides of the ∆PQR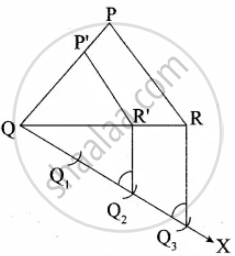

Steps of construction:

(i) Construct a ∆PQR with any measurement.

(ii) Draw a ray QX making an acute angle with QR on the side opposite to the vertex P.

(iii) Locate 3 points Q₁, Q₂ and Q₃ on QX.

So that QQ₁ = Q₁Q₂ = Q₂Q₃

(iv) Join Q₃ R and draw a line through Q₂ parallel to Q₃ R to intersect QR at R’.

(v) Draw a line through R’ parallel to the line RP to intersect QP at P’. Then ∆P’QR’ is the required triangle.