Advertisements
Advertisements
प्रश्न
Construct a triangle similar to a given triangle PQR with its sides equal to `2/3` of the corresponding sides of the triangle PQR (scale factor `2/3 < 1`)
उत्तर
Given ∆PQR, we are required to construct another triangle whose sides are `2/3` of the corresponding sides of the ∆PQR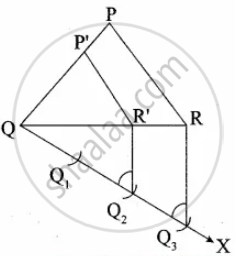
Steps of construction:
(i) Construct a ∆PQR with any measurement.
(ii) Draw a ray QX making an acute angle with QR on the side opposite to the vertex P.
(iii) Locate 3 points Q1, Q2 and Q3 on QX.
So that QQ1 = Q1Q2 = Q2Q3
(iv) Join Q3 R and draw a line through Q2 parallel to Q3 R to intersect QR at R’.
(v) Draw a line through R’ parallel to the line RP to intersect QP at P’. Then ∆P’QR’ is the required triangle.
APPEARS IN
संबंधित प्रश्न
E and F are points on the sides PQ and PR, respectively, of a ΔPQR. For the following case, state whether EF || QR.
PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
Show that ΔABC, where A(–2, 0), B(2, 0), C(0, 2) and ΔPQR where P(–4, 0), Q(4, 0), R(0, 2) are similar triangles
In triangle ABC, AD is perpendicular to side BC and AD2 = BD × DC. Show that angle BAC = 90°.
In the given figure, if ∠ADE = ∠B, show that ΔADE ~ ΔABC. If AD = 3.8cm, AE = 3.6cm, BE = 2.1cm and BC = 4.2cm, find DE.
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and ∠ABC = 90°.
Calculate : the actual lengths of AB and BC in km.
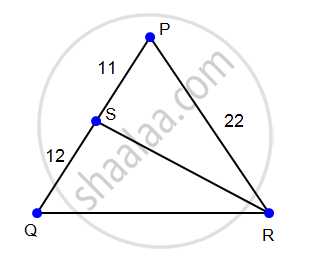
In the following figure, in Δ PQR, seg RS is the bisector of ∠PRQ.
PS = 11, SQ = 12, PR = 22. Find QR.
In the figure, PQR is a straight line and PS || RT. If QS = 12cm, QR = 15cm, QT = 10cm and RT = 6cm, find PQ and PS.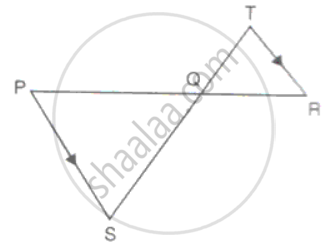
Prove that the external bisector of an angle of a triangle divides the opposite side externally n the ratio of the sides containing the angle.
In ΔABC, DE is drawn parallel to BC cutting AB in the ratio 2 : 3. Calculate:
(i) `("area"(Δ"ADE"))/("area"(Δ"ABC")`
(i) `("area"("trapeziumEDBC"))/("area"(Δ"ABC"))`
A map is drawn to scale of 1:20000. Find: The distance covered by 6cm on the map
