Advertisements
Advertisements
प्रश्न
Construct a triangle similar to a given triangle PQR with its sides equal to `2/3` of the corresponding sides of the triangle PQR (scale factor `2/3 < 1`)
उत्तर
Given ∆PQR, we are required to construct another triangle whose sides are `2/3` of the corresponding sides of the ∆PQR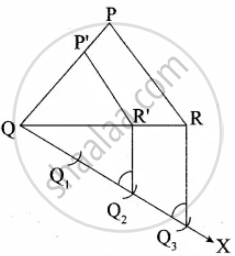
Steps of construction:
(i) Construct a ∆PQR with any measurement.
(ii) Draw a ray QX making an acute angle with QR on the side opposite to the vertex P.
(iii) Locate 3 points Q1, Q2 and Q3 on QX.
So that QQ1 = Q1Q2 = Q2Q3
(iv) Join Q3 R and draw a line through Q2 parallel to Q3 R to intersect QR at R’.
(v) Draw a line through R’ parallel to the line RP to intersect QP at P’. Then ∆P’QR’ is the required triangle.
APPEARS IN
संबंधित प्रश्न
In the given figure, ΔOAB ~ ΔOCD. If AB = 8cm, BO = 6.4cm, OC = 3.5cm and CD = 5cm, find (i) OA (ii) DO.
In a circle, two chords AB and CD intersect at a point P inside the circle. Prove that
(a) ΔPAC ∼PDB (b) PA. PB= PC.PD

The areas of two similar triangles ABC and PQR are in the ratio 9:16. If BC = 4.5cm, find the length of QR.
State the SSS-similarity criterion for similarity of triangles
Prove that the area of Δ BCE described on one side BC of a square ABCD is one half the area of the similar Δ ACF described on the diagonal AC.
In Δ ABC, DE || BC; DC and EB intersects at F. if `"DE"/"BC" = 2/7` , find `("Ar" (triangle "FDE"))/("Ar" (triangle "FBC"))`
A triangle LMN has been reduced by scale factor 0.8 to the triangle L' M' N'. Calculate: the length of LM, if L' M' = 5.4 cm.
Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half of the area of similar triangle ACF described on the diagonal AC as base.
In the given figure ABC and CEF are two triangles where BA is parallel to CE and AF: AC = 5: 8.
(i) Prove that ΔADF ∼ ΔCEF
(ii) Find AD if CE = 6 cm
(iii) If DF is parallel to BC find area of ΔADF: area of ΔABC.
In the figure, PQR is a straight line and PS || RT. If QS = 12cm, QR = 15cm, QT = 10cm and RT = 6cm, find PQ and PS.
