Advertisements
Advertisements
प्रश्न
Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half of the area of similar triangle ACF described on the diagonal AC as base.
उत्तर
ABCD is a square. ∆BCE is described on side BC is similar to ∆ACF described on diagonal AC.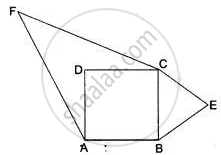
Since ABCD is a square. Therefore,
AB = BC = CD = DA
and AC = `sqrt(2)"BC"` ...[∵ Diagonal = `sqrt(2)` (side)]
Now, ∆BCE ~ ∆ACF
⇒ `"Area (∆BCE)"/"Area (∆ACF)" = "BC"^2/"AC"^2`
⇒ `"Area (∆BCE)"/"Area (∆ACF)" = "BF"^2/(sqrt(2)"BC")^2 = (1)/(2)`
⇒ Area (∆BCE) = `(1)/(2) "area (∆ACF)"`.
Hence proved.
APPEARS IN
संबंधित प्रश्न
The diagonals of a quadrilateral ABCD intersect each other at the point O such that `("AO")/("BO") = ("CO")/("DO")`. Show that ABCD is a trapezium.
The given diagram shows two isosceles triangles which are similar. In the given diagram, PQ and BC are not parallel; PC = 4, AQ = 3, QB = 12, BC = 15 and AP = PQ.

Calculate:
- the length of AP,
- the ratio of the areas of triangle APQ and triangle ABC.
In the given figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and the distance between AB and AC is 14 cm. If arcs of equal radii 7 cm taking A, B, C and D as centres, have been drawn, then find the area of the shaded region ?

D and E are points on the sides AB and AC respectively of Δ ABC such that AB=5.6cm, AD= 1.4cm, AC=7 .2cm and AE = 1.5 cm, show that DE is parallel to BC
A triangle ABC has been enlarged by scale factor m = 2.5 to the triangle A' B' C'. Calculate : the length of AB, if A' B' = 6 cm.
Points A(3, 1), B(5, 1), C(a, b) and D(4, 3) are vertices of a parallelogram ABCD. Find the values of a and b.
In the figure, PR || SQ. If PR = 10cm, PT = 5cm, TQ = 6cm and ST = 9cm, calculate RT and SQ.
Construct a triangle similar to a given triangle PQR with its sides equal to `7/3` of the corresponding sides of the triangle PQR (scale factor `7/3 > 1`)
In given fig., quadrilateral PQRS, side PQ || side SR, AR = 5 AP, then prove that, SR = 5PQ
An architecture have model of building. Length of building is 1 m then length of model is 0.75 cm. Then find length and height of model building whose actual length is 22.5 m and height is 10 m
