Advertisements
Advertisements
प्रश्न
Construct a triangle similar to a given triangle PQR with its sides equal to `7/3` of the corresponding sides of the triangle PQR (scale factor `7/3 > 1`)
उत्तर
Given triangle ABC, we are required to construct another triangle whose sides are `7/3` of the corresponding sides of the ∆ABC.
Steps of construction:
(i) Construct a ∆PQR with any measurement.
(ii) Draw a ray QX making an acute angle with QR on the side opposite to the vertex P.
(iii) Locate 7 points Q1, Q2, Q3, Q4, Q5, Q6, Q7 on QX.
So that QQ1 = Q1Q2 = Q2Q3 = Q3Q4 = Q5Q6 = Q6Q7 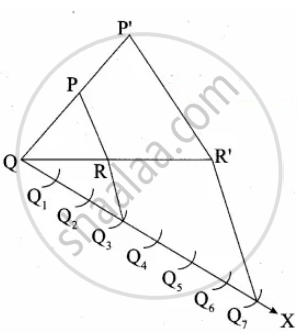
(iv) Join Q3 to R and draw a line through Q7 parallel to Q3 R intersecting the extended line segment QR at R’.
(v) Draw a line parallel to RP. Intersecting the extended line segment QP at P’.
∴ ∆P’QR’ is the required triangle.
APPEARS IN
संबंधित प्रश्न
Given `triangle ABC ~ triangle PQR`, if `(AB)/(PQ) = 1/3`, then find `(ar triangle ABC)/(ar triangle PQR)`
In the given figure, ΔODC~ΔOBA, ∠BOC = 115° and ∠CDO = 700.
Find (i) ∠DCO (ii) ∠DCO (iii) ∠OAB (iv) ∠OBA.

In an isosceles ΔABC, the base AB is produced both ways in P and Q such that
AP × BQ = AC2.
Prove that ΔACP~ΔBCQ.

The areas of two similar triangles are 169cm2 and 121cm2 respectively. If the longest side of the larger triangle is 26cm, find the longest side of the smaller triangle.
In Δ ABC , MN || BC .

If BC = 14 cm and MN = 6 cm , find `("Ar" triangle "AMN")/("Ar" . ("trapezium MBCN"))`
A model of a ship is made with a scale factor of 1 : 500. Find
The length of the ship, if the model length is 60 cm.
If ΔABC ~ ΔPQR and ∠A = 60°, then ∠P = ?
Prove that, if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
Find the scale factor in each of the following and state the type of size transformation:
Image length = 8cm, Actual length = 20cm.
A model of a ship is made to a scale of 1:500. Find: The area other deck o the ship, if the area of the deck of its model is m2
