Advertisements
Advertisements
प्रश्न
Prove that the area of the triangle BCE described on one side BC of a square ABCD as base is one half of the area of similar triangle ACF described on the diagonal AC as base.
उत्तर
ABCD is a square. ∆BCE is described on side BC is similar to ∆ACF described on diagonal AC.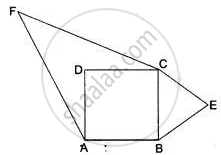
Since ABCD is a square. Therefore,
AB = BC = CD = DA
and AC = `sqrt(2)"BC"` ...[∵ Diagonal = `sqrt(2)` (side)]
Now, ∆BCE ~ ∆ACF
⇒ `"Area (∆BCE)"/"Area (∆ACF)" = "BC"^2/"AC"^2`
⇒ `"Area (∆BCE)"/"Area (∆ACF)" = "BF"^2/(sqrt(2)"BC")^2 = (1)/(2)`
⇒ Area (∆BCE) = `(1)/(2) "area (∆ACF)"`.
Hence proved.
APPEARS IN
संबंधित प्रश्न
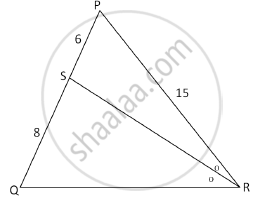
In the following figure, in ΔPQR, seg RS is the bisector of ∠PRQ. If PS = 6, SQ = 8, PR = 15, find QR.
In ΔABC, ∠ABC = ∠DAC, AB = 8 cm, AC = 4 cm and AD = 5 cm.
- Prove that ΔACD is similar to ΔBCA.
- Find BC and CD.
- Find area of ΔACD : area of ΔABC.

If in ∆DEF and ∆PQR, ∠D ≅ ∠Q, ∠R ≅ ∠E then which of the following statements is false?

A line PQ is drawn parallel to the side BC of ΔABC which cuts side AB at P and side AC at Q. If AB = 9.0 cm, CA = 6.0 cm and AQ = 4.2 cm, find the length of AP.
The diagonal AC of a parallelogram ABCD intersects DP at the point Q, where P is any point on side AB. Prove that CQ x PQ = QA x QD.
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The base area of the truck, if the base area of the model is 30m2
In the given figure YH || TE. Prove that ΔWHY ~ ΔWET and also find HE and TE
Are triangles in figure similar? If yes, then write the test of similarity.
Two triangles are similar. Smaller triangle’s sides are 4 cm, 5 cm, 6 cm. Perimeter of larger triangle is 90 cm then find the sides of larger triangle.
In the given figure, if ABCD is a trapezium in which AB || CD || EF, then prove that `(AE)/(ED) = (BF)/(FC)`.

