Advertisements
Advertisements
प्रश्न
In figure ABC and DBC are two triangles on the same base BC. Prove that
`"Area (ΔABC)"/"Area (ΔDBC)" = "AO"/"DO"`.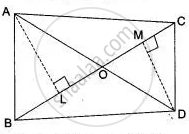
उत्तर
In ΔAOL and ΔDOM
∠ALO = ∠DMO, ...(90° each)
∠AOL = ∠DOM,
(Vertically opposite 2 sides)
(Vert. opp-angles)
∴ ΔAOL ∼ ΔDOM
∴ `"AL"/"DM" = "AO"/"DO"` ...(1)
If two Δ's are similar the ratio between their corresponding sides is the same.
Now, `"area (ΔABC)"/"area (ΔDBC)" = ((1)/(2) xx "BC" xx "AL")/((1)/(2) xx "BC" xx "Dm") = "AL"/"DM"`
From (1), we get
`"area (ΔABC)"/"area (ΔDBC)" = "AO"/"DO"`.
Hence proved.
APPEARS IN
संबंधित प्रश्न
State, true or false:
The diagonals of a trapezium divide each other into proportional segments.
In quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE : EC = BE : ED. Show that: ABCD is a trapezium.
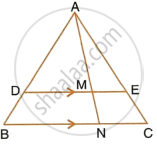
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm. Find lengths of ME and DM.
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that: CB : BA = CP : PA
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.
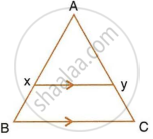
Find :
- `(AY)/(YC)`
- `(YC)/(AC)`
- XY
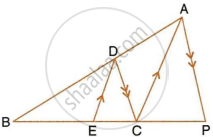
In the following figure, DE || AC and DC || AP. Prove that : `(BE)/(EC) = (BC)/(CP)`.
Triangles ABC and DEF are similar.
If area (ΔABC) = 16 cm, area (ΔDEF) = 25 cm2 and BC = 2.3 cm find EF.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
In ΔABC, and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and angle ABC = 90°.
Calculate:
- the actual lengths of AB and BC in km.
- the area of the plot in sq. km.
