Advertisements
Advertisements
प्रश्न
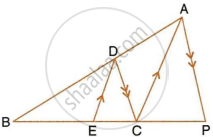
In the following figure, DE || AC and DC || AP. Prove that : `(BE)/(EC) = (BC)/(CP)`.
उत्तर
In the given figure,
DE || AC and DC || AP
To prove: `(BE)/(EC) = (BC)/(CP)`
Proof: In ΔBCA, we have
ED || CA
Since a line drawn is || to one side of a Δ divides the other two side proportionality.
∴ `(BE)/(EC) = (BD)/(DA)` ...(i)
Similarly in ΔBPA; we have DC || AP
Since a line drawn is || to one side of a Δ divides the other two side proportionality.
∴ `(BC)/(CP) = (BD)/(DA)` ...(ii)
From (i) and (ii),
`(BE)/(EC) = (BC)/(CP)`
Hence proved.
APPEARS IN
संबंधित प्रश्न
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm. Find lengths of ME and DM.
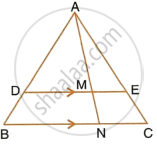
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.
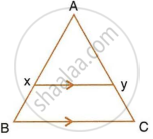
Find :
- `(AY)/(YC)`
- `(YC)/(AC)`
- XY
In the following figure, AB, CD and EF are perpendicular to the straight line BDF.
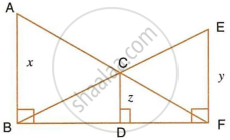
If AB = x and CD = z unit and EF = y unit, prove that : `1/x + 1/y = 1/z`
Triangle ABC is similar to triangle PQR. If AD and PM are altitudes of the two triangles, prove that : `(AB)/(PQ) = (AD)/(PM)`.
In the given figure, AB and DE are perpendiculars to BC.
Find the ratio of the area of a ΔABC : area of ΔDEC.

ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :

ΔADE ~ ΔACB.
In the figure below, PB and QA are perpendiculars to the line segment AB. If PO = 6 cm, QO = 9 cm and the area of ΔPOB = 120 cm2, find the area of ΔQOA.
Triangles ABC and DEF are similar.
If area (ΔABC) = 9 cm2, area (ΔDEF) = 64 cm2 and BC = 5·1 cm find AB.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEf) = 64 cm2 and DE = 6.2 cm, find AB.
