Advertisements
Advertisements
प्रश्न
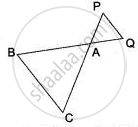
In the figure below, PB and QA are perpendiculars to the line segment AB. If PO = 6 cm, QO = 9 cm and the area of ΔPOB = 120 cm2, find the area of ΔQOA.
उत्तर
PO = 6 cm, QO = 9 cm.
Area of ΔPOB = 120
In ΔPOB and ΔQOB,
∠B = ∠A ...(each 90°)
∠POB = ∠QOA ...(Opposite vertical angel)
∴ ΔPOB ∼ ΔQOA
In similar Δ's `"Area of ΔQOA"/"Area of ΔPOB" = "OQ"^2/"OP"^2`
`"Area of ΔQOA"/(120) = 9^2/6^2`
Area of ΔQOA = `(81 xx 120)/(36)`
= 27 x 10
Area of ΔQOA = 270 cm2.
APPEARS IN
संबंधित प्रश्न
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.
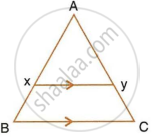
Find : XY
Triangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and bisector of angle QPR meets QR at point M, prove that : `(AB)/(PQ) = (AD)/(PM)`.
In the following figure, ∠AXY = ∠AYX. If `(BX)/(AX) = (CY)/(AY)`, show that triangle ABC is isosceles.
In the figure given below, AB ‖ EF ‖ CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm. Calculate : AC
In the given figure, AB and DE are perpendiculars to BC.
If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
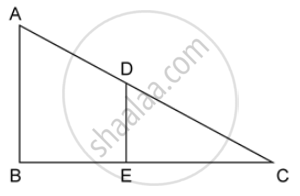
In the given figure, AB and DE are perpendiculars to BC.
Find the ratio of the area of a ΔABC : area of ΔDEC.

ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :

ΔADE ~ ΔACB.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
In the adjoining figure, ΔACB ∼ ∆APQ. If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm and AP = 2.8 cm find the area (∆ACB) : area (∆APQ).