Advertisements
Advertisements
प्रश्न
In the adjoining figure, ΔACB ∼ ∆APQ. If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm and AP = 2.8 cm find the area (∆ACB) : area (∆APQ).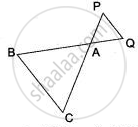
उत्तर
∆ACB ∼ ∆APQ.
Then, `"area (∆ACB)"/"area (∆APQ)" = "BC"^2/"PQ"^2`
= `(10)^2/(5)^2`
= `(100)/(25)`
= `(4)/(1)`
Required ratio is 4 : 1.
APPEARS IN
संबंधित प्रश्न
In quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE : EC = BE : ED. Show that: ABCD is a trapezium.
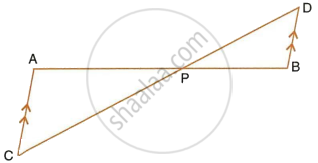
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that: ΔAPC and ΔBPD are similar.
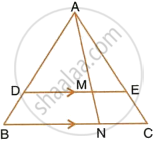
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm. Find lengths of ME and DM.
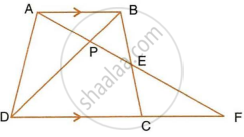
In the following figure, ABCD to a trapezium with AB || DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm, Calculate: AF
Triangle ABC is similar to triangle PQR. If AD and PM are altitudes of the two triangles, prove that : `(AB)/(PQ) = (AD)/(PM)`.
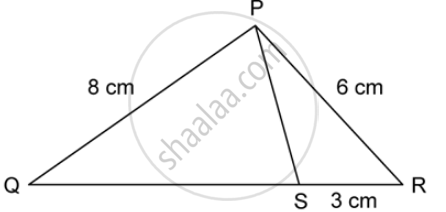
PQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR = ∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.
- i. ProveΔPQR∼ Δ
- Find the lengths of QR and PS.
- `(Area of DeltaPQR)/(area of Delta SPR)`
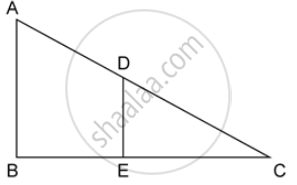
In the given figure, AB and DE are perpendiculars to BC.
Prove that : ΔABC ~ ΔDEC
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
In ΔABC, and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.
In the given figure ΔABC and ΔAMP are right angled at B and M respectively.
Given AC = 10 cm, AP = 15 cm and PM = 12 cm.
(i) Prove ΔABC ∼ Δ AMP.
(ii) Find AB and BC.
