Advertisements
Advertisements
प्रश्न
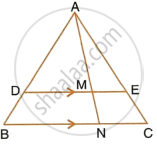
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm. Find lengths of ME and DM.
उत्तर
In ΔAME and ΔANC,
∠AME = ∠ANC ...(Since DE || BC that is, ME || NC)
∠MAE = ∠NAC ...(Common angle)
`=>` ΔAME and ΔANC ...(AA criterion for similarity)
`=> (ME)/(NC) = (AE)/(AC)`
`=> (ME)/6 = 15/24`
`=>` ME = 3.75 cm
In ΔADE and ΔABC,
∠ADE = ∠ABC ...(Since DE || BC that is, ME || NC)
∠AED = ∠ACB ...(Since DE || BC)
`=>` ΔADE and ΔABC ...(AA criterion for similarity)
`=> (AD)/(AB) = (AE)/(AC) = 15/24` ...(i)
In ΔADM and ΔABN,
∠ADM = ∠ABN ...(Since DE || BC that is, ME || NC)
∠DAM = ∠BAN ...(Common angle)
`=>` ΔADM and ΔABN ...(AA criterion for similarity)
`=> (DM)/(BN) = (AD)/(AB) = 15/24` ...(From (i))
`=> (DM)/24 = 15/24`
`=>` DM = 15 cm
APPEARS IN
संबंधित प्रश्न
Angle BAC of triangle ABC is obtuse and AB = AC. P is a point in BC such that PC = 12 cm. PQ and PR are perpendiculars to sides AB and AC respectively. If PQ = 15 cm and PR = 9 cm; find the length of PB.
In the given figure, AB || DC, BO = 6 cm and DQ = 8 cm; find: BP × DO.

In the given figure, AD = AE and AD2 = BD × EC. Prove that: triangles ABD and CAE are similar.
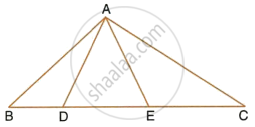
Triangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and bisector of angle QPR meets QR at point M, prove that : `(AB)/(PQ) = (AD)/(PM)`.
In the given figure, AB and DE are perpendiculars to BC.
Find the ratio of the area of a ΔABC : area of ΔDEC.

ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
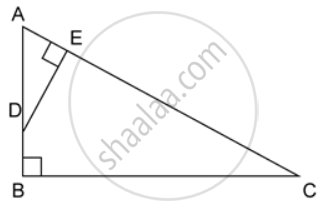
If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
In the figure below, PB and QA are perpendiculars to the line segment AB. If PO = 6 cm, QO = 9 cm and the area of ΔPOB = 120 cm2, find the area of ΔQOA.
Triangles ABC and DEF are similar.
If area (ΔABC) = 16 cm2, area (ΔDEF) = 25 cm2 and BC = 2·3 cm find EF.
Triangles ABC and DEF are similar.
If area (ΔABC) = 9 cm2, area (ΔDEF) = 64 cm2 and BC = 5·1 cm find AB.
Triangles ABC and DEF are similar.
If AC = 19 cm and DF = 8 cm, find the ratio between the areas of two triangles.
