Advertisements
Advertisements
प्रश्न
Triangles ABC and DEF are similar.
If area (ΔABC) = 9 cm2, area (ΔDEF) = 64 cm2 and BC = 5·1 cm find AB.
उत्तर
We have
area (ΔABC) = 9 cm2
area (ΔDEF) = 64 cm2
and DE = 5·1 cm
Since, `"area (ΔABC)"/"area (ΔDEF)" = "AB"^2/"DE"^2`
⇒ `(9)/(64) = "AB"^2/"DE"^2`
⇒ `"AB"/"DE" = (3)/(8)`
⇒ `"AB"/(5·1) = (3)/(8)`
⇒ AB = `(3)/(8) xx 5.1 = (15·3)/(8)`
⇒ AB = 1·9125 cm.
APPEARS IN
संबंधित प्रश्न
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that: DL : DP = AL : DC.
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that: AB × BC = BP × CA
In the following figure, AB, CD and EF are perpendicular to the straight line BDF.
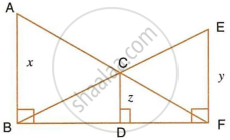
If AB = x and CD = z unit and EF = y unit, prove that : `1/x + 1/y = 1/z`
Triangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and bisector of angle QPR meets QR at point M, prove that : `(AB)/(PQ) = (AD)/(PM)`.
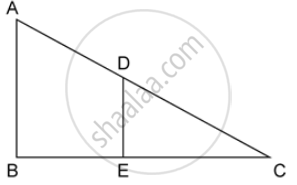
In the given figure, AB and DE are perpendiculars to BC.
Prove that : ΔABC ~ ΔDEC
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
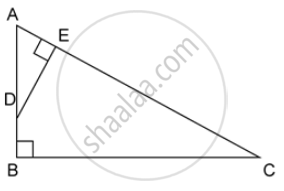
Find, area of ΔADE : area of quadrilateral BCED.
Triangles ABC and DEF are similar.
If area (ΔABC) = 16 cm, area (ΔDEF) = 25 cm2 and BC = 2.3 cm find EF.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
In ΔABC, and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.
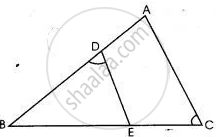
In the given figure ABC is a triangle with ∠EDB = ∠ACB.
(i) Prove that ΔABC ∼ ΔEBD.
(ii) If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of ΔBED = 9 cm2. Calculate the length of AB and area of ΔABC.