Advertisements
Advertisements
प्रश्न
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that: DL : DP = AL : DC.
उत्तर
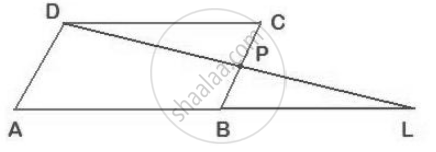
Since AD || BC, that is, AD || BP,
By the basic proportionality theorem, we get
`(DL)/(DP) = (AL)/(AB)`
Since ABCD is a parallelogram, AB = DC
So, `(DL)/(DP) = (AL)/(DC)`
APPEARS IN
संबंधित प्रश्न
State, true or false:
Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
State, true or false:
The diagonals of a trapezium divide each other into proportional segments.
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that: If BD = 2.4 cm, AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm; find the lengths of PA and PC.
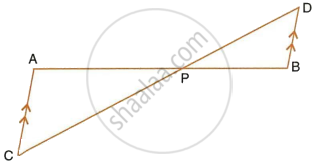
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that: AB × BC = BP × CA
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
In the following figure, AB, CD and EF are perpendicular to the straight line BDF.
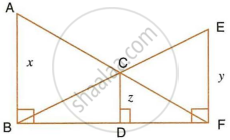
If AB = x and CD = z unit and EF = y unit, prove that : `1/x + 1/y = 1/z`
In the figure given below, AB || EF || CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm.
Calculate :
- EF
- AC
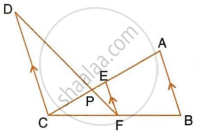
In the given figure, AB and DE are perpendiculars to BC.
Prove that : ΔABC ~ ΔDEC
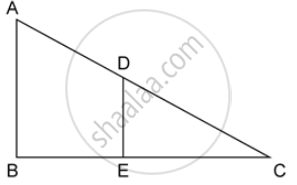
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
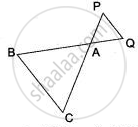
In the adjoining figure, ΔACB ∼ ∆APQ. If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm and AP = 2.8 cm find the area (∆ACB) : area (∆APQ).