Advertisements
Advertisements
Question
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that: DL : DP = AL : DC.
Solution
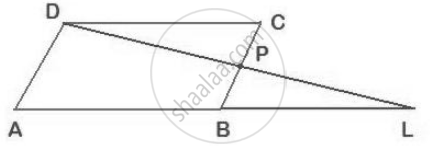
Since AD || BC, that is, AD || BP,
By the basic proportionality theorem, we get
`(DL)/(DP) = (AL)/(AB)`
Since ABCD is a parallelogram, AB = DC
So, `(DL)/(DP) = (AL)/(DC)`
APPEARS IN
RELATED QUESTIONS
State, true or false:
Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
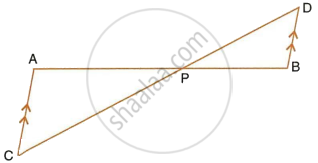
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that: ΔAPC and ΔBPD are similar.
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that: AB × BC = BP × CA
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.
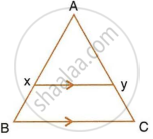
Find :
- `(AY)/(YC)`
- `(YC)/(AC)`
- XY
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.
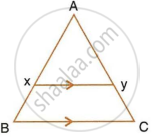
Find : XY
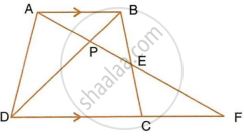
In the following figure, ABCD to a trapezium with AB || DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm, Calculate: AF
In ΔABC, and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.
In the adjoining figure ABC is a right angle triangle with ∠BAC = 90°, and AD ⊥ BC.
(i) Prove ΔADB ∼ ΔCDA.
(ii) If BD = 18 cm, CD = 8 cm find AD.
(iii) Find the ratio of the area of ΔADB is to area of ΔCDA.
In the figure below, PB and QA are perpendiculars to the line segment AB. If PO = 6 cm, QO = 9 cm and the area of ΔPOB = 120 cm2, find the area of ΔQOA.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEf) = 64 cm2 and DE = 6.2 cm, find AB.
