Advertisements
Advertisements
Question
In the adjoining figure ABC is a right angle triangle with ∠BAC = 90°, and AD ⊥ BC.
(i) Prove ΔADB ∼ ΔCDA.
(ii) If BD = 18 cm, CD = 8 cm find AD.
(iii) Find the ratio of the area of ΔADB is to area of ΔCDA.
Solution
(i) In ΔADB and ΔADC
AD = AD ...(self)
∠ADC = 90° ...(AD ⊥ BC)
∠ADB = 90° ...(AD ⊥ BC)
then ∠ADC = ∠ADB
so, ΔADB ∼ ΔADC ...(By AAA similarity)
or ΔADB ∼ ΔCDA
Hence proved.
(ii) ∵ ΔADB ∼ ΔCDA
∴ `"AD"/"BD" = "CD"/"AD"`
`("corresponding parts of similar Δ's are proportional")`
or
AD2 = BD x CD
⇒ AD2 = 18 x 8 ...`(("BD" = 18),("CD" = 8),("(given)"))`
⇒ AD2 = 144
AD = 12 cm
(iii) `"Area of ΔADB"/"Area of ΔCDA" = "BD"^2/"AD"^2`
`("Area theorem of similar triangles")`
= `18^2/12^2 = (18 xx 18)/(12 xx 12)`
= `(3 xx 3)/(2 xx 2) = (9)/(4)`
⇒ area (ΔADB) : area (ΔCDA) = 9 : 4.
APPEARS IN
RELATED QUESTIONS
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that: ΔAPC and ΔBPD are similar.
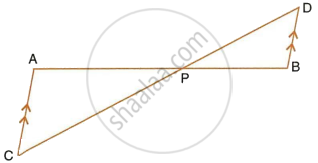
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that : PA x PD = PB x PC.
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm. Find lengths of ME and DM.
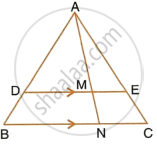
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.

Find : `(YC)/(AC)`
Triangle ABC is similar to triangle PQR. If AD and PM are corresponding medians of the two triangles, prove that : `("AB")/("PQ") = ("AD")/("PM")`.
Triangle ABC is similar to triangle PQR. If AD and PM are altitudes of the two triangles, prove that : `(AB)/(PQ) = (AD)/(PM)`.
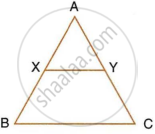
In the following figure, ∠AXY = ∠AYX. If `(BX)/(AX) = (CY)/(AY)`, show that triangle ABC is isosceles.
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :

ΔADE ~ ΔACB.
In figure ABC and DBC are two triangles on the same base BC. Prove that
`"Area (ΔABC)"/"Area (ΔDBC)" = "AO"/"DO"`.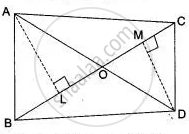
Triangles ABC and DEF are similar.
If area (ΔABC) = 9 cm2, area (ΔDEF) = 64 cm2 and BC = 5·1 cm find AB.
