Advertisements
Advertisements
Question
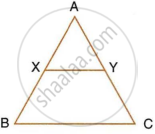
In the following figure, ∠AXY = ∠AYX. If `(BX)/(AX) = (CY)/(AY)`, show that triangle ABC is isosceles.
Solution
In the given figure,
∠AXY = ∠AYX
And `(BX)/(AX) = (CY)/(AY)`
To prove: ΔABC is an isosceles triangle
In ΔAXY
∠AXY = ∠AYX ...(Given)
∴ AY = AX ...(Sides opposite to equal angles)
`(BX)/(AX) = (CY)/(AY) => (AX)/(BX) = (AY)/(CY)`
∴ XY || BC
∴ ∠B = ∠AXY and ∠C = ∠AYX ...(Corresponding angles)
But ∠AXY = ∠AYX is given
∴ ∠B = ∠C
∴ AC = AB ...(Side opposite to equal angles)
∴ ΔABC is an isosceles triangle.
APPEARS IN
RELATED QUESTIONS
State, true or false:
Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
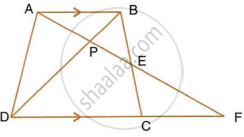
In the following figure, ABCD to a trapezium with AB ‖ DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm, Calculate: PE
Triangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and bisector of angle QPR meets QR at point M, prove that : `(AB)/(PQ) = (AD)/(PM)`.
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :

ΔADE ~ ΔACB.
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
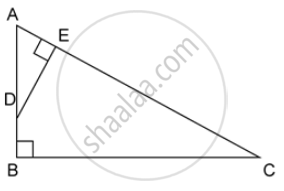
Find, area of ΔADE : area of quadrilateral BCED.
Triangles ABC and DEF are similar.
If AC = 19 cm and DF = 8 cm, find the ratio between the area of two triangles.
In figure ABC and DBC are two triangles on the same base BC. Prove that
`"Area (ΔABC)"/"Area (ΔDBC)" = "AO"/"DO"`.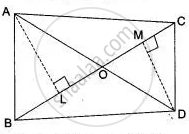
In the adjoining figure, ΔACB ∼ ∆APQ. If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm and AP = 2.8 cm find the area (∆ACB) : area (∆APQ).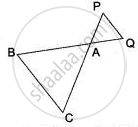
Triangles ABC and DEF are similar.
If area (ΔABC) = 9 cm2, area (ΔDEF) = 64 cm2 and BC = 5·1 cm find AB.
Triangles ABC and DEF are similar.
If AC = 19 cm and DF = 8 cm, find the ratio between the areas of two triangles.
