Advertisements
Advertisements
Question
Triangle ABC is similar to triangle PQR. If AD and PM are corresponding medians of the two triangles, prove that : `("AB")/("PQ") = ("AD")/("PM")`.
Solution
Given, ΔABC ∼ ΔPQR; AD and PM are the medians of ΔABC and ΔPQR respectively.
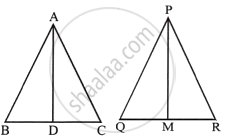
To prove: `("AB")/("PQ") = ("AD")/("PM")`
Proof: Since, ΔABC ∼ ΔPQR
∴ ∠B = ∠Q and
`("AB")/("PQ") = ("BC")/("QR") = (2"BD")/(2"QM") = ("BD")/("QM")` ...(∵ D and M are mid-points of BC and QR)
Now in ΔABD and ΔPQM
`("AB")/("PQ") = ("BD")/("QM")` ...(Proved)
∠B = ∠Q ...(Given)
∴ ΔABD ∼ ΔPQM ...(SAS axiom of similarity)
∴ `("AB")/("PQ") = ("AD")/("PM")` ...(Corresponding sides of Δ's are proportional)
APPEARS IN
RELATED QUESTIONS
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that: DP : PL = DC : BL.
In the given figure, AB || DC, BO = 6 cm and DQ = 8 cm; find: BP × DO.

In the given figure, AD = AE and AD2 = BD × EC. Prove that: triangles ABD and CAE are similar.
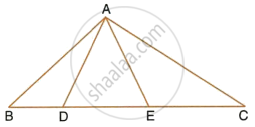
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that: AB × BC = BP × CA
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.

Find : `(YC)/(AC)`
In the following figure, DE || AC and DC || AP. Prove that : `(BE)/(EC) = (BC)/(CP)`.
Triangles ABC and DEF are similar.
If AC = 19 cm and DF = 8 cm, find the ratio between the area of two triangles.
In the adjoining figure, ΔACB ∼ ∆APQ. If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm and AP = 2.8 cm find the area (∆ACB) : area (∆APQ).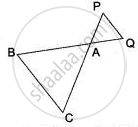
In the given figure ΔABC and ΔAMP are right angled at B and M respectively.
Given AC = 10 cm, AP = 15 cm and PM = 12 cm.
(i) Prove ΔABC ∼ Δ AMP.
(ii) Find AB and BC.
