Advertisements
Advertisements
Question
In the given figure, AD = AE and AD2 = BD × EC. Prove that: triangles ABD and CAE are similar.
Solution
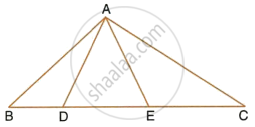
In the given figure,
AD = AE
AD2 = BD × EC
To prove: ΔABD ~ ΔCAE
Proof: In ΔADC, AD = AE
∴ ∠ADE = ∠AED ...(Angles opposite to equal sides)
But ∠ADE + ∠ADB
= ∠AED + ∠AEC
= 180°
∴ ∠ADB = ∠AEC
AD2 = BD × EC
`(AD)/(BD) = (EC)/(AD)`
`\implies (AE)/(BD) = (EC)/(AD)` ...(∵ AD = AE)
And ∠ADB = ∠AEC
∴ ΔABD ~ ΔCAE ...(SAS axiom)
APPEARS IN
RELATED QUESTIONS
State, true or false:
Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
State, true or false:
The diagonals of a trapezium divide each other into proportional segments.
Angle BAC of triangle ABC is obtuse and AB = AC. P is a point in BC such that PC = 12 cm. PQ and PR are perpendiculars to sides AB and AC respectively. If PQ = 15 cm and PR = 9 cm; find the length of PB.
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.

Find : `(YC)/(AC)`
Triangle ABC is similar to triangle PQR. If AD and PM are altitudes of the two triangles, prove that : `(AB)/(PQ) = (AD)/(PM)`.
Triangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and bisector of angle QPR meets QR at point M, prove that : `(AB)/(PQ) = (AD)/(PM)`.
In the given figure, AB and DE are perpendiculars to BC.
Prove that : ΔABC ~ ΔDEC
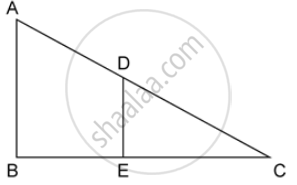
In the given figure, AB and DE are perpendiculars to BC.
If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
Triangles ABC and DEF are similar.
If area (ΔABC) = 16 cm2, area (ΔDEF) = 25 cm2 and BC = 2·3 cm find EF.
