State, true or false: The diagonals of a trapezium divide each other into proportional segments. - Mathematics

State, true or false:

The diagonals of a trapezium divide each other into proportional segments.

MCQ

True or False

This statement is True.

shaalaa.com

Areas of Similar Triangles Are Proportional to the Squares on Corresponding Sides

Is there an error in this question or solution?

Chapter 15 Similarity (With Applications to Maps and Models)
Exercise 15 (A) | Q 11.7 | Page 213

In quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE : EC = BE : ED. Show that: ABCD is a trapezium.

In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that :

P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that: DP : PL = DC : BL.

In the given figure, AD = AE and AD² = BD × EC. Prove that: triangles ABD and CAE are similar.

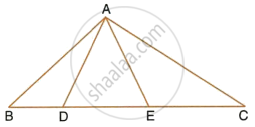
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm. Find lengths of ME and DM.

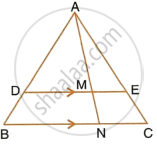
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.

In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that: AB × BC = BP × CA

Triangle ABC is similar to triangle PQR. If AD and PM are corresponding medians of the two triangles, prove that : `("AB")/("PQ") = ("AD")/("PM")`.

Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm², area (ΔDEF) = 64 cm² and DE = 6.2 cm, find AB.