Advertisements
Advertisements
Question
In quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE : EC = BE : ED. Show that: ABCD is a trapezium.
Solution
Given, AE : EC = BE : ED
Draw EF || AB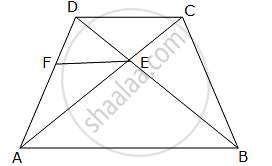
In ∆ABD, EF || AB
Using Basic Proportionality theorem,
`(DF)/(FA) = (DE)/(EB)`
But, given `(DE)/(EB) = (CE)/(EA)`
∴ `(DF)/(FA) = (CE)/(EA)`
Thus, in ∆DCA, E and F are points on CA and DA respectively such that
`(DF)/(FA) = (CE)/(EA)`
Thus, by converse of Basic proportionality theorem, FE || DC.
But, FE || AB.
Hence, AB || DC.
Thus, ABCD is a trapezium.
APPEARS IN
RELATED QUESTIONS
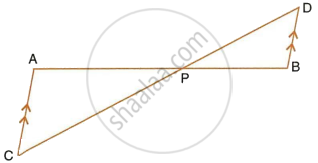
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that: If BD = 2.4 cm, AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm; find the lengths of PA and PC.
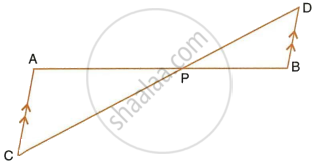
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that: ΔAPC and ΔBPD are similar.
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that : PA x PD = PB x PC.
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that: DP : PL = DC : BL.
In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that: OA × OD = OB × OC.
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that: AB × BC = BP × CA
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
In the following figure, ABCD to a trapezium with AB ‖ DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm, Calculate: PE
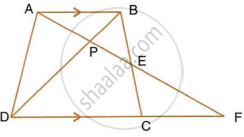
In the figure given below, AB || EF || CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm.
Calculate :
- EF
- AC
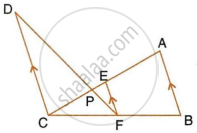
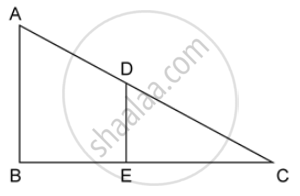
In the given figure, AB and DE are perpendiculars to BC.
If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.