Advertisements
Advertisements
Question
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that : PA x PD = PB x PC.
Solution

In ΔAPB and ΔCPD,
∠APB = ∠CPD .......(vertically opposite angles)
∠ABP = ∠CDP ....(alternate angles since AC || DC)
ΔAPB ∼ ΔCPD .....(AA criterion for similarity)
`=> (PA)/(PC) = (PB)/(PD)` .....(Since corresponding sides of similar triangles are equal)
`=>` PA x PD = PB x PC
APPEARS IN
RELATED QUESTIONS
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that: If BD = 2.4 cm, AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm; find the lengths of PA and PC.
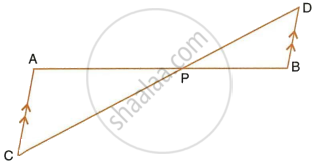
Angle BAC of triangle ABC is obtuse and AB = AC. P is a point in BC such that PC = 12 cm. PQ and PR are perpendiculars to sides AB and AC respectively. If PQ = 15 cm and PR = 9 cm; find the length of PB.
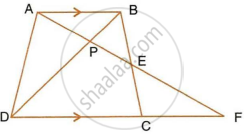
In the following figure, ABCD to a trapezium with AB || DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm.
Calculate:
- EC
- AF
- PE
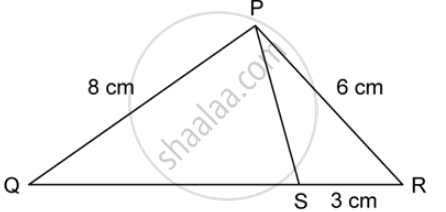
PQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR = ∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.
- i. ProveΔPQR∼ Δ
- Find the lengths of QR and PS.
- `(Area of DeltaPQR)/(area of Delta SPR)`
In the given figure, AB and DE are perpendiculars to BC.
If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
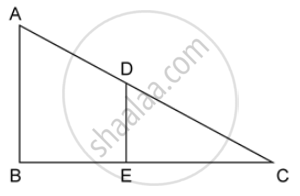
In the given figure, AB and DE are perpendiculars to BC.
Find the ratio of the area of a ΔABC : area of ΔDEC.

Triangles ABC and DEF are similar.
If area (ΔABC) = 9 cm2, area (ΔDEF) = 64 cm2 and DE = 5.1 cm, find AB.
In figure ABC and DBC are two triangles on the same base BC. Prove that
`"Area (ΔABC)"/"Area (ΔDBC)" = "AO"/"DO"`.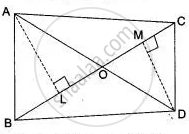
In the adjoining figure ABC is a right angle triangle with ∠BAC = 90°, and AD ⊥ BC.
(i) Prove ΔADB ∼ ΔCDA.
(ii) If BD = 18 cm, CD = 8 cm find AD.
(iii) Find the ratio of the area of ΔADB is to area of ΔCDA.
Triangles ABC and DEF are similar.
If area (ΔABC) = 9 cm2, area (ΔDEF) = 64 cm2 and BC = 5·1 cm find AB.
