Advertisements
Advertisements
प्रश्न
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that : PA x PD = PB x PC.
उत्तर

In ΔAPB and ΔCPD,
∠APB = ∠CPD .......(vertically opposite angles)
∠ABP = ∠CDP ....(alternate angles since AC || DC)
ΔAPB ∼ ΔCPD .....(AA criterion for similarity)
`=> (PA)/(PC) = (PB)/(PD)` .....(Since corresponding sides of similar triangles are equal)
`=>` PA x PD = PB x PC
APPEARS IN
संबंधित प्रश्न
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that: DP : PL = DC : BL.
In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that: OA × OD = OB × OC.
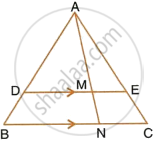
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.
- Write all possible pairs of similar triangles.
- Find lengths of ME and DM.
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.
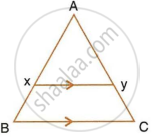
Find : XY
In the following figure, DE || AC and DC || AP. Prove that : `(BE)/(EC) = (BC)/(CP)`.
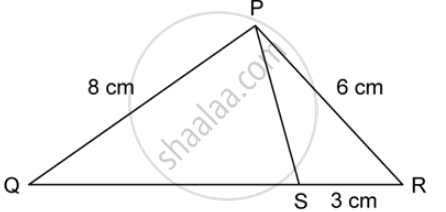
PQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR = ∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.
- i. ProveΔPQR∼ Δ
- Find the lengths of QR and PS.
- `(Area of DeltaPQR)/(area of Delta SPR)`
In figure ABC and DBC are two triangles on the same base BC. Prove that
`"Area (ΔABC)"/"Area (ΔDBC)" = "AO"/"DO"`.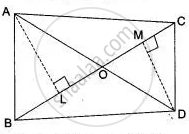
In ΔABC, and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.
In the adjoining figure ABC is a right angle triangle with ∠BAC = 90°, and AD ⊥ BC.
(i) Prove ΔADB ∼ ΔCDA.
(ii) If BD = 18 cm, CD = 8 cm find AD.
(iii) Find the ratio of the area of ΔADB is to area of ΔCDA.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEf) = 64 cm2 and DE = 6.2 cm, find AB.
