Advertisements
Advertisements
प्रश्न
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.
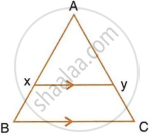
Find : XY
उत्तर
In ΔAXY and ΔABC,
∠XAY = ∠BAC ...(Common angle)
∠AXY = ∠ABC ...(Corresponding angles for parallel lines, XY || BC)
∠AYX = ∠ACB ...(Corresponding angles for parallel lines, XY || BC)
Thus, ΔAXY ∼ ΔABC
Hence, `(AX)/(AB) = (XY)/(BC)` ...(Using similar triangle property)
`(AX)/(AX + XB) = (XY)/18`
`9/(9 + 4.5) = (XY)/18`
`XY = (18 xx 9)/(13.5)`
XY = 12 cm
APPEARS IN
संबंधित प्रश्न
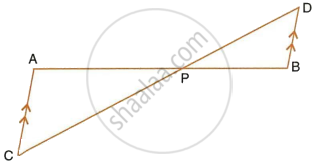
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that: If BD = 2.4 cm, AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm; find the lengths of PA and PC.
In the given figure, AB || DC, BO = 6 cm and DQ = 8 cm; find: BP × DO.

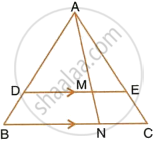
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm. Find lengths of ME and DM.
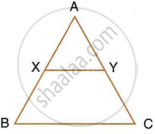
In the following figure, ∠AXY = ∠AYX. If `(BX)/(AX) = (CY)/(AY)`, show that triangle ABC is isosceles.
In the figure given below, AB || EF || CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm.
Calculate :
- EF
- AC
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
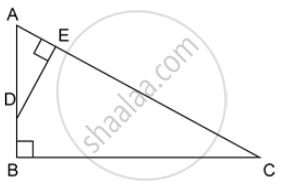
Find, area of ΔADE : area of quadrilateral BCED.
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
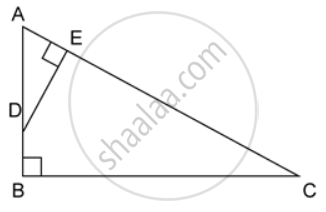
If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
In ΔABC, and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEf) = 64 cm2 and DE = 6.2 cm, find AB.
