Advertisements
Advertisements
प्रश्न
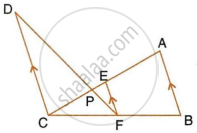
In the figure given below, AB || EF || CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm.
Calculate :
- EF
- AC
उत्तर
In the given figure,
AB || EF || CD
AB = 22.5 cm, EP = 7.5 cm
PC = 15 cm and DC = 27 cm
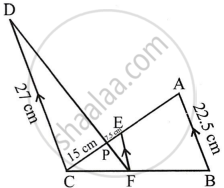
To calculate:
- EF
- AC
In ΔDCP and ΔPEF
∠CPD = ∠EPF ...(Vertically opposite angles)
∠DCP = ∠PEF ...(Alternate angles)
∴ ΔDCP ∼ ΔPEF ...(AA axiom)
∴ `(DC)/(EF) = (CP)/(PE)`
`\implies 27/(EF) = 15/7.5`
`\implies EF = (27 xx 7.5)/15`
= `27/2`
= 13.5 cm
Similarly in ΔABC, EF || AB
∴ ΔCEF ∼ ΔACB
∴ `(CE)/(AC) = (EF)/(AB)`
`22.5/(AC) = 13.5/22.5`
`AC = (22.5 xx 22.5)/13.5`
= `(225 xx 225)/(135 xx 10 xx 10)`
= `375/10`
= 37.5 cm
Thus AC = 37.5 cm
APPEARS IN
संबंधित प्रश्न
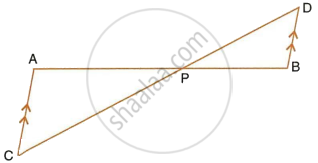
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that: ΔAPC and ΔBPD are similar.
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that : PA x PD = PB x PC.
In the given figure, AD = AE and AD2 = BD × EC. Prove that: triangles ABD and CAE are similar.
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that: AB × BC = BP × CA
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.
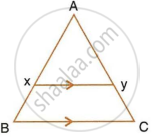
Find : XY
In the following figure, AB, CD and EF are perpendicular to the straight line BDF.
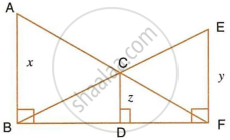
If AB = x and CD = z unit and EF = y unit, prove that : `1/x + 1/y = 1/z`
Triangles ABC and DEF are similar.
If area (ΔABC) = 9 cm2, area (ΔDEF) = 64 cm2 and DE = 5.1 cm, find AB.
In figure ABC and DBC are two triangles on the same base BC. Prove that
`"Area (ΔABC)"/"Area (ΔDBC)" = "AO"/"DO"`.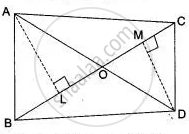
Triangles ABC and DEF are similar.
If AC = 19 cm and DF = 8 cm, find the ratio between the areas of two triangles.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEf) = 64 cm2 and DE = 6.2 cm, find AB.
