Advertisements
Advertisements
प्रश्न
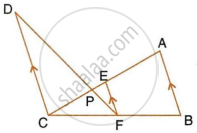
In the figure given below, AB || EF || CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm.
Calculate :
- EF
- AC
उत्तर
In the given figure,
AB || EF || CD
AB = 22.5 cm, EP = 7.5 cm
PC = 15 cm and DC = 27 cm
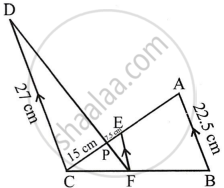
To calculate:
- EF
- AC
In ΔDCP and ΔPEF
∠CPD = ∠EPF ...(Vertically opposite angles)
∠DCP = ∠PEF ...(Alternate angles)
∴ ΔDCP ∼ ΔPEF ...(AA axiom)
∴ `(DC)/(EF) = (CP)/(PE)`
`\implies 27/(EF) = 15/7.5`
`\implies EF = (27 xx 7.5)/15`
= `27/2`
= 13.5 cm
Similarly in ΔABC, EF || AB
∴ ΔCEF ∼ ΔACB
∴ `(CE)/(AC) = (EF)/(AB)`
`22.5/(AC) = 13.5/22.5`
`AC = (22.5 xx 22.5)/13.5`
= `(225 xx 225)/(135 xx 10 xx 10)`
= `375/10`
= 37.5 cm
Thus AC = 37.5 cm
APPEARS IN
संबंधित प्रश्न
In quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE : EC = BE : ED. Show that: ABCD is a trapezium.
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that : PA x PD = PB x PC.
In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that: ΔAOB is similar to ΔCOD.
In ΔABC; BM ⊥ AC and CN ⊥ AB; show that:
`(AB)/(AC) = (BM)/(CN) = (AM)/(AN)`
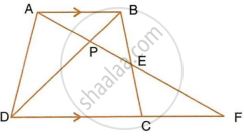
In the following figure, ABCD to a trapezium with AB || DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm, Calculate: AF
Triangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and bisector of angle QPR meets QR at point M, prove that : `(AB)/(PQ) = (AD)/(PM)`.
In the following figure, DE || AC and DC || AP. Prove that : `(BE)/(EC) = (BC)/(CP)`.
In the given figure, AB and DE are perpendiculars to BC.
Find the ratio of the area of a ΔABC : area of ΔDEC.

Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
Triangles ABC and DEF are similar.
If AC = 19 cm and DF = 8 cm, find the ratio between the areas of two triangles.
