Advertisements
Advertisements
प्रश्न
In ΔABC; BM ⊥ AC and CN ⊥ AB; show that:
`(AB)/(AC) = (BM)/(CN) = (AM)/(AN)`
उत्तर
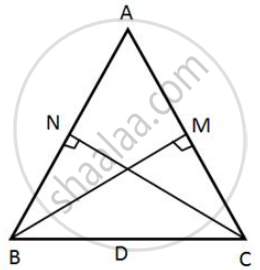
In ΔABM and ΔACN,
∠AMB = ∠ANC ...(BM ⊥ AC and CN ⊥ AB)
∠BAM = ∠CAN ...(Common angle)
`=>` ΔABM ∼ ΔACN ...(AA criterion for similarity)
`=> (AB)/(AC) = (BM)/(CN) = (AM)/(AN)`
APPEARS IN
संबंधित प्रश्न
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that : PA x PD = PB x PC.
In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that: ΔAOB is similar to ΔCOD.
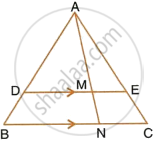
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.
- Write all possible pairs of similar triangles.
- Find lengths of ME and DM.
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that: AB × BC = BP × CA
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.
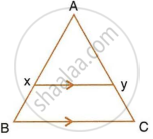
Find :
- `(AY)/(YC)`
- `(YC)/(AC)`
- XY
Triangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and bisector of angle QPR meets QR at point M, prove that : `(AB)/(PQ) = (AD)/(PM)`.
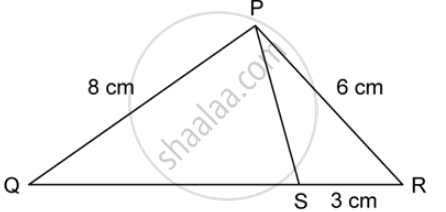
PQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR = ∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.
- i. ProveΔPQR∼ Δ
- Find the lengths of QR and PS.
- `(Area of DeltaPQR)/(area of Delta SPR)`
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :

ΔADE ~ ΔACB.
Two isosceles triangle have equal vertical angles and their areas are in the ratio of 36 : 25. Find the ratio between their corresponding heights.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEf) = 64 cm2 and DE = 6.2 cm, find AB.
