Advertisements
Advertisements
प्रश्न
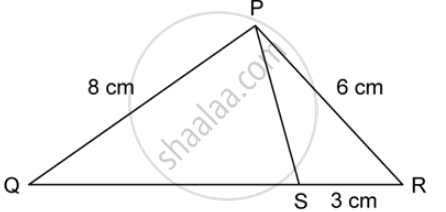
PQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR = ∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.
- i. ProveΔPQR∼ Δ
- Find the lengths of QR and PS.
- `(Area of DeltaPQR)/(area of Delta SPR)`
उत्तर
i. In ∆PQR and ∆SPR,
∠PSR = ∠QPR … given
∠PRQ = ∠PRS … common angle
⇒ ∆PQR ∼ ∆SPR (AA Test)
ii. Find the lengths of QR and PS.
Since ∆PQR ∼ ∆SPR … from (i)
`=> (PQ)/(SP) = (QR)/(PR) = (PR)/(SR)` ....(a)
`(QR)/(PR) = (PR)/(SR)` ....from (a)
`=> (QR)/6 = 6/3`
`=> QR = (6 xx 6)/3 = 12 cm`
`(PQ)/(SP) = (PR)/(SR)` ....from (a)
`=> 8/(SP) = 6/3`
`=> SP = (8 xx 3)/6 = 4cm`
iii. `(area of DeltaPQR)/(area of Delta SPR) = (PQ^2)/(SP^2) = (8^2)/(4^2) = 64/16 = 4`
APPEARS IN
संबंधित प्रश्न
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that: DP : PL = DC : BL.
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.

Find : `(YC)/(AC)`
In the following figure, ABCD to a trapezium with AB || DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm.
Calculate:
- EC
- AF
- PE
In the following figure, AB, CD and EF are perpendicular to the straight line BDF.
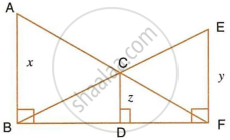
If AB = x and CD = z unit and EF = y unit, prove that : `1/x + 1/y = 1/z`
Triangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and bisector of angle QPR meets QR at point M, prove that : `(AB)/(PQ) = (AD)/(PM)`.
In the given figure, AB and DE are perpendiculars to BC.
If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
Triangles ABC and DEF are similar.
If area (ΔABC) = 9 cm2, area (ΔDEF) = 64 cm2 and DE = 5.1 cm, find AB.
In ΔABC, and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.
In the given figure ABC is a triangle with ∠EDB = ∠ACB.
(i) Prove that ΔABC ∼ ΔEBD.
(ii) If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of ΔBED = 9 cm2. Calculate the length of AB and area of ΔABC.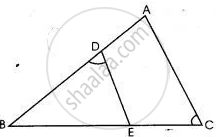
In the given figure ΔABC and ΔAMP are right angled at B and M respectively.
Given AC = 10 cm, AP = 15 cm and PM = 12 cm.
(i) Prove ΔABC ∼ Δ AMP.
(ii) Find AB and BC.
