Advertisements
Advertisements
प्रश्न
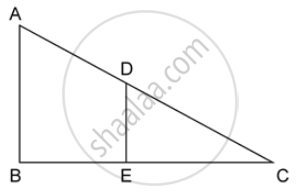
In the following figure, ABCD to a trapezium with AB || DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm.
Calculate:
- EC
- AF
- PE
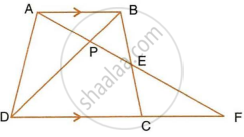
उत्तर
i. In ΔAEB and ΔFEC,
∠AEB = ∠FEC ...(Vertically opposite angles)
∠BAE = ∠CFE ...(Since AB || DC)
ΔAEB ∼ ΔAFEC ...(AA criterion for similarity)
`=> (AE)/(FE) = (BE)/(CE) = (AB)/(FC)`
`=> 15/(CE) = 9/13.5`
`=>` CE = 22.5 cm
ii. In ΔAPB and ΔFPD
∠APB = ∠FPD ...(Vertically opposite angles)
∠BAP = ∠DFP ...(Since AB || DF)
ΔAPB ∼ ΔFPD ...(AA criterion for similarity)
`=> (AP)/(FP) = (AB)/(FD)`
`=> 6/(FP) = 9/31.5`
`=>` FP = 21 cm
So AF = AP + PF
= 6 + 21
= 27 cm
iii. Given: ABCD is trapezium, AB || DC
AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm, BE = 15 cm
Consider ΔAPB and ΔFPD,
`=>` ∠APB = ∠FPD ...(Vertically opposite angles)
`=>` ∠BAP = ∠DFP ...(Since AB || DF)
ΔAPB ~ ΔFPD ...(AA criterion for similarity)
`=> (AP)/(FP) = (AB)/(FD)`
`=> 6/(FP) = 9/31.5`
`=>` FP = 21 cm
So, AF = AP + PF
= 6 + 21
= 27 cm
In ΔAEB and ΔFEC,
∠AEB = ∠FEC ...(Vertically opposite angles)
∠BAF = ∠CFE ...(Since AB || DC)
ΔAEB ~ ΔFEC ...(AA criterion for Similarity)
`=> (AF)/(FE) = (AB)/(FC)`
`=> (AP + PE)/(FE) = 9/13.5`
`=> (AP + PE)/(FE) = 90/135`
`=> (6 + PE)/(FE) = 30/45 = 2/3`
`=>` 3(6 + PE) = 2FE
`=> (3(6 + PE))/2 = FE`
Now, PF = PE + EF
`21 = PE + (3 (6 + PE))/2`
`21 = (2PE + 18 + 3PE)/2`
42 = 5PE + 18
42 – 18 = 5PE
24 = 5PE
`24/5` = PE
PE = 4.8
APPEARS IN
संबंधित प्रश्न
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that: DL : DP = AL : DC.
In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that: OA × OD = OB × OC.
In ΔABC; BM ⊥ AC and CN ⊥ AB; show that:
`(AB)/(AC) = (BM)/(CN) = (AM)/(AN)`
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
In the following figure, ABCD to a trapezium with AB || DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm, Calculate: AF
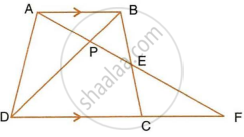
In the figure given below, AB || EF || CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm.
Calculate :
- EF
- AC
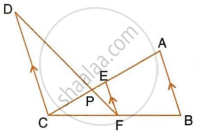
In the figure given below, AB ‖ EF ‖ CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm. Calculate : AC
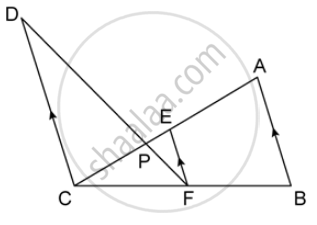
In the given figure, AB and DE are perpendiculars to BC.
If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
In the given figure ABC is a triangle with ∠EDB = ∠ACB.
(i) Prove that ΔABC ∼ ΔEBD.
(ii) If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of ΔBED = 9 cm2. Calculate the length of AB and area of ΔABC.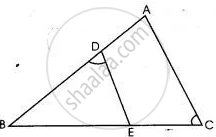
Triangles ABC and DEF are similar.
If area (ΔABC) = 9 cm2, area (ΔDEF) = 64 cm2 and BC = 5·1 cm find AB.
