Advertisements
Advertisements
प्रश्न
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
उत्तर
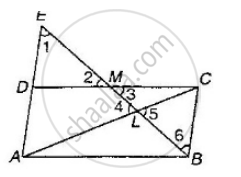
∠1 = ∠6 (Alternate interior angles)
∠2 = ∠3 (Vertically opposite angles)
DM = MC (M is the mid-point of CD)
ΔDEM ≅ ΔCBM (AAS Congruence criterion)
So, DE = BC (Corresponding parts of congruent triangles)
Also, AD = BC (Opposite sides of a parallelogram)
AE = AD + DE = 2BC
Now, ∠1 = ∠6 and ∠4 = ∠5
ΔELA ∼ ΔBLC (AA similarity)
`=> (EL)/(BL) = (EA)/(BC)`
`=> (EL)/(BL) = (2BC)/(BC) = 2`
`=>` EL = 2BL
APPEARS IN
संबंधित प्रश्न
In quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE : EC = BE : ED. Show that: ABCD is a trapezium.
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that: DL : DP = AL : DC.
In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that: ΔAOB is similar to ΔCOD.
In the following figure, ABCD to a trapezium with AB || DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm.
Calculate:
- EC
- AF
- PE
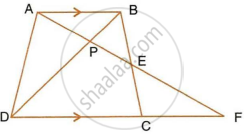
In the following figure, DE || AC and DC || AP. Prove that : `(BE)/(EC) = (BC)/(CP)`.
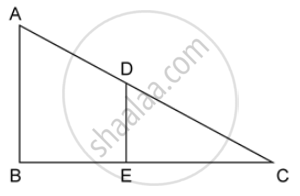
In the given figure, AB and DE are perpendiculars to BC.
If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
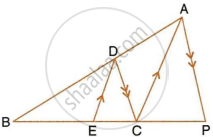
Two isosceles triangle have equal vertical angles and their areas are in the ratio of 36 : 25. Find the ratio between their corresponding heights.
In the figure below, PB and QA are perpendiculars to the line segment AB. If PO = 6 cm, QO = 9 cm and the area of ΔPOB = 120 cm2, find the area of ΔQOA.
Triangles ABC and DEF are similar.
If AC = 19 cm and DF = 8 cm, find the ratio between the areas of two triangles.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEf) = 64 cm2 and DE = 6.2 cm, find AB.
