Advertisements
Advertisements
प्रश्न
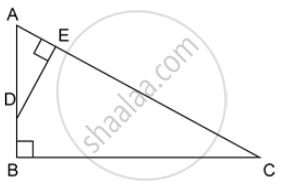
In the given figure, AB and DE are perpendiculars to BC.
Find the ratio of the area of a ΔABC : area of ΔDEC.

उत्तर
In ΔABC and ΔDEC,
∠ABC = ∠DEC ...(both are right angles)
∠ACB = ∠DCE ....(common angles)
ΔABC ∼ ΔDEC ...(AA criterion for similarity)
`=> (ar (DeltaABC))/(ar (DeltaDEC)) = (AB^2)/(DE^2) = (6^2)/(4^2) = 36/16`
`=> (ar (DeltaABC))/(ar (DeltaDEC)) = 9/4`
APPEARS IN
संबंधित प्रश्न
In quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE : EC = BE : ED. Show that: ABCD is a trapezium.
Angle BAC of triangle ABC is obtuse and AB = AC. P is a point in BC such that PC = 12 cm. PQ and PR are perpendiculars to sides AB and AC respectively. If PQ = 15 cm and PR = 9 cm; find the length of PB.
In the given figure, AD = AE and AD2 = BD × EC. Prove that: triangles ABD and CAE are similar.
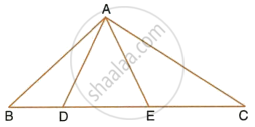
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm. Find lengths of ME and DM.
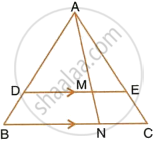
In the following figure, ABCD to a trapezium with AB || DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm, Calculate: AF
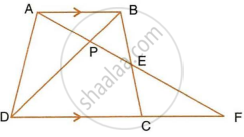
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
Find, area of ΔADE : area of quadrilateral BCED.
Triangles ABC and DEF are similar.
If area (ΔABC) = 16 cm, area (ΔDEF) = 25 cm2 and BC = 2.3 cm find EF.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
In figure ABC and DBC are two triangles on the same base BC. Prove that
`"Area (ΔABC)"/"Area (ΔDBC)" = "AO"/"DO"`.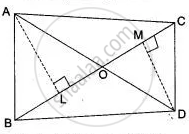
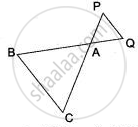
In the adjoining figure, ΔACB ∼ ∆APQ. If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm and AP = 2.8 cm find the area (∆ACB) : area (∆APQ).