Advertisements
Advertisements
प्रश्न
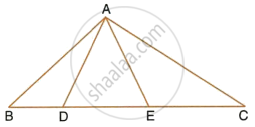
In the given figure, AD = AE and AD2 = BD × EC. Prove that: triangles ABD and CAE are similar.
उत्तर
In the given figure,
AD = AE
AD2 = BD × EC
To prove: ΔABD ~ ΔCAE
Proof: In ΔADC, AD = AE
∴ ∠ADE = ∠AED ...(Angles opposite to equal sides)
But ∠ADE + ∠ADB
= ∠AED + ∠AEC
= 180°
∴ ∠ADB = ∠AEC
AD2 = BD × EC
`(AD)/(BD) = (EC)/(AD)`
`\implies (AE)/(BD) = (EC)/(AD)` ...(∵ AD = AE)
And ∠ADB = ∠AEC
∴ ΔABD ~ ΔCAE ...(SAS axiom)
APPEARS IN
संबंधित प्रश्न
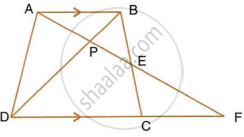
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that :
- ΔAPB is similar to ΔCPD.
- PA × PD = PB × PC.
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that : PA x PD = PB x PC.
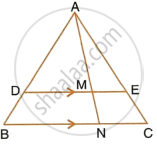
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm. Find lengths of ME and DM.
In the following figure, ABCD to a trapezium with AB ‖ DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm, Calculate: PE
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
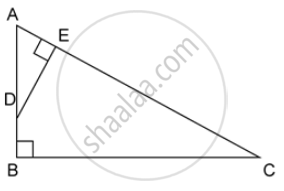
Find, area of ΔADE : area of quadrilateral BCED.
In figure ABC and DBC are two triangles on the same base BC. Prove that
`"Area (ΔABC)"/"Area (ΔDBC)" = "AO"/"DO"`.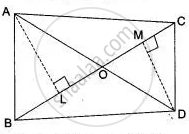
In the adjoining figure ABC is a right angle triangle with ∠BAC = 90°, and AD ⊥ BC.
(i) Prove ΔADB ∼ ΔCDA.
(ii) If BD = 18 cm, CD = 8 cm find AD.
(iii) Find the ratio of the area of ΔADB is to area of ΔCDA.
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and angle ABC = 90°.
Calculate:
- the actual lengths of AB and BC in km.
- the area of the plot in sq. km.
In the figure below, PB and QA are perpendiculars to the line segment AB. If PO = 6 cm, QO = 9 cm and the area of ΔPOB = 120 cm2, find the area of ΔQOA.
Triangles ABC and DEF are similar.
If area (ΔABC) = 16 cm2, area (ΔDEF) = 25 cm2 and BC = 2·3 cm find EF.
