Advertisements
Advertisements
प्रश्न
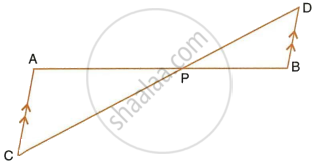
In the given figure, AB || DC, BO = 6 cm and DQ = 8 cm; find: BP × DO.

उत्तर
In ΔDOQ and ΔBOP,
∠QDO = ∠PBO ...(Since AB || DC that is, PB || DQ)
So, ∠DOQ = ∠BOP ...(Vertically opposite angles)
`=>` ΔDOQ ∼ ΔBOP ...(AA criterion for similarity)
`=> (DO)/(BO) = (DQ)/(BP)`
`=> (DO)/6 = 8/(BP)`
`=>` BP × DO = 8 × 6 = 48 cm2
APPEARS IN
संबंधित प्रश्न
State, true or false:
Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
In quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE : EC = BE : ED. Show that: ABCD is a trapezium.
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that: If BD = 2.4 cm, AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm; find the lengths of PA and PC.
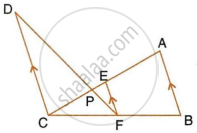
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that :
- ΔAPB is similar to ΔCPD.
- PA × PD = PB × PC.
Angle BAC of triangle ABC is obtuse and AB = AC. P is a point in BC such that PC = 12 cm. PQ and PR are perpendiculars to sides AB and AC respectively. If PQ = 15 cm and PR = 9 cm; find the length of PB.
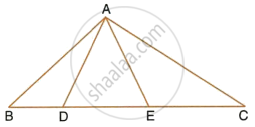
In the given figure, AD = AE and AD2 = BD × EC. Prove that: triangles ABD and CAE are similar.
Triangle ABC is similar to triangle PQR. If AD and PM are altitudes of the two triangles, prove that : `(AB)/(PQ) = (AD)/(PM)`.
In the figure given below, AB || EF || CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm.
Calculate :
- EF
- AC
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
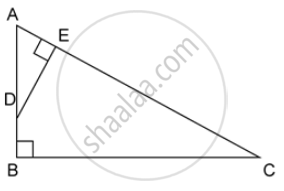
Find, area of ΔADE : area of quadrilateral BCED.
In the figure below, PB and QA are perpendiculars to the line segment AB. If PO = 6 cm, QO = 9 cm and the area of ΔPOB = 120 cm2, find the area of ΔQOA.
