Advertisements
Advertisements
प्रश्न
Triangle ABC is similar to triangle PQR. If AD and PM are altitudes of the two triangles, prove that : `(AB)/(PQ) = (AD)/(PM)`.
उत्तर
Given, ΔABC ∼ ΔPQR
AD and PM are altitudes of these two triangles
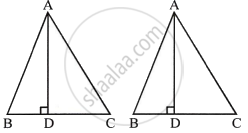
To prove: `(AB)/(PQ) = (AD)/(PM)`
Proof: Since, ΔABC ∼ ΔPQR
∴ ∠B = ∠Q
`(AB)/(PQ) = (BC)/(QR)`
Now in ΔABD and ΔPQM
∠B = ∠Q
∠D = ∠M ...(Each 90°)
∴ ΔABD ∼ ΔPQM ...(AAS axiom)
∴ `(AB)/(PQ) = (AD)/(PM)` ...(Corresponding sides of Δ's are proportional)
APPEARS IN
संबंधित प्रश्न
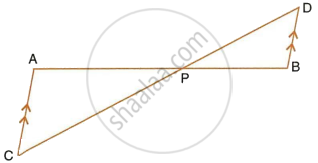
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that: ΔAPC and ΔBPD are similar.
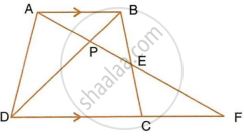
In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that: OA × OD = OB × OC.
In the given figure, AB || DC, BO = 6 cm and DQ = 8 cm; find: BP × DO.

In the following figure, ABCD to a trapezium with AB || DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm, Calculate: AF
In the following figure, AB, CD and EF are perpendicular to the straight line BDF.
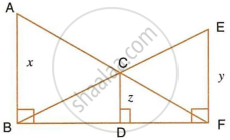
If AB = x and CD = z unit and EF = y unit, prove that : `1/x + 1/y = 1/z`
In the figure given below, AB ‖ EF ‖ CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm. Calculate : AC
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
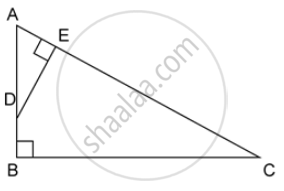
Find, area of ΔADE : area of quadrilateral BCED.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
Triangles ABC and DEF are similar.
If area (ΔABC) = 16 cm2, area (ΔDEF) = 25 cm2 and BC = 2·3 cm find EF.
