Advertisements
Advertisements
प्रश्न
Triangles ABC and DEF are similar.
If AC = 19 cm and DF = 8 cm, find the ratio between the areas of two triangles.
उत्तर
In ΔABC and ΔDEF, AC = 19 cm, DF = 8 cm.
Since, `"area (ΔABC)"/"area (ΔDEF)" = "AC"^2/"DF"^2 = (19)^2/(8)^2 = (361)/(64)`
Hence, the required ratio is 361: 64.
APPEARS IN
संबंधित प्रश्न
In quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE : EC = BE : ED. Show that: ABCD is a trapezium.
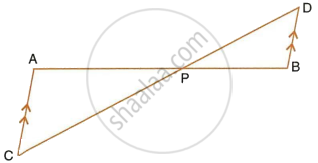
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that: ΔAPC and ΔBPD are similar.
Angle BAC of triangle ABC is obtuse and AB = AC. P is a point in BC such that PC = 12 cm. PQ and PR are perpendiculars to sides AB and AC respectively. If PQ = 15 cm and PR = 9 cm; find the length of PB.
In ΔABC; BM ⊥ AC and CN ⊥ AB; show that:
`(AB)/(AC) = (BM)/(CN) = (AM)/(AN)`
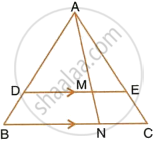
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm. Find lengths of ME and DM.
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that: AB × BC = BP × CA
Triangle ABC is similar to triangle PQR. If AD and PM are altitudes of the two triangles, prove that : `(AB)/(PQ) = (AD)/(PM)`.
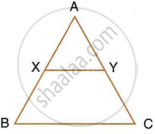
In the following figure, ∠AXY = ∠AYX. If `(BX)/(AX) = (CY)/(AY)`, show that triangle ABC is isosceles.
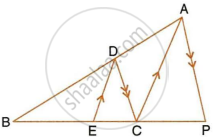
In the following figure, DE || AC and DC || AP. Prove that : `(BE)/(EC) = (BC)/(CP)`.
In the figure below, PB and QA are perpendiculars to the line segment AB. If PO = 6 cm, QO = 9 cm and the area of ΔPOB = 120 cm2, find the area of ΔQOA.
