Advertisements
Advertisements
प्रश्न
In quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE : EC = BE : ED. Show that: ABCD is a trapezium.
उत्तर
Given, AE : EC = BE : ED
Draw EF || AB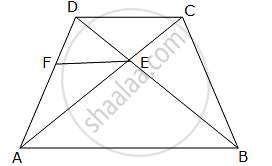
In ∆ABD, EF || AB
Using Basic Proportionality theorem,
`(DF)/(FA) = (DE)/(EB)`
But, given `(DE)/(EB) = (CE)/(EA)`
∴ `(DF)/(FA) = (CE)/(EA)`
Thus, in ∆DCA, E and F are points on CA and DA respectively such that
`(DF)/(FA) = (CE)/(EA)`
Thus, by converse of Basic proportionality theorem, FE || DC.
But, FE || AB.
Hence, AB || DC.
Thus, ABCD is a trapezium.
APPEARS IN
संबंधित प्रश्न
State, true or false:
Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
In ΔABC; BM ⊥ AC and CN ⊥ AB; show that:
`(AB)/(AC) = (BM)/(CN) = (AM)/(AN)`
In the given figure, AD = AE and AD2 = BD × EC. Prove that: triangles ABD and CAE are similar.
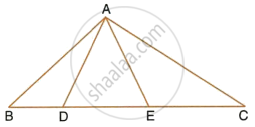
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm. Find lengths of ME and DM.
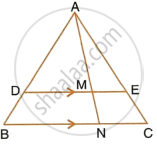
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.

Find : `(YC)/(AC)`
Triangle ABC is similar to triangle PQR. If AD and PM are altitudes of the two triangles, prove that : `(AB)/(PQ) = (AD)/(PM)`.
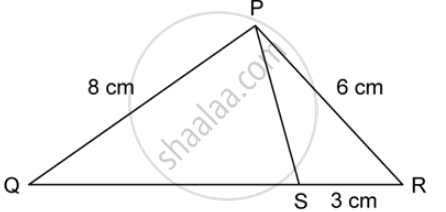
PQR is a triangle. S is a point on the side QR of ΔPQR such that ∠PSR = ∠QPR. Given QP = 8 cm, PR = 6 cm and SR = 3 cm.
- i. ProveΔPQR∼ Δ
- Find the lengths of QR and PS.
- `(Area of DeltaPQR)/(area of Delta SPR)`
In ΔABC, and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.
In the figure below, PB and QA are perpendiculars to the line segment AB. If PO = 6 cm, QO = 9 cm and the area of ΔPOB = 120 cm2, find the area of ΔQOA.
