Advertisements
Advertisements
प्रश्न
State, true or false:
Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
पर्याय
True
False
उत्तर
This statement is True.
APPEARS IN
संबंधित प्रश्न
In ΔABC; BM ⊥ AC and CN ⊥ AB; show that:
`(AB)/(AC) = (BM)/(CN) = (AM)/(AN)`
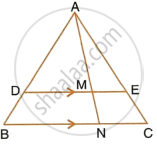
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm. Find lengths of ME and DM.
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that: AB × BC = BP × CA
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.

Find : `(YC)/(AC)`
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.
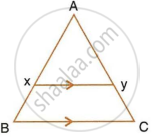
Find : XY
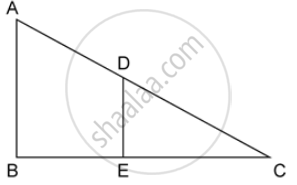
In the given figure, AB and DE are perpendiculars to BC.
Prove that : ΔABC ~ ΔDEC
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
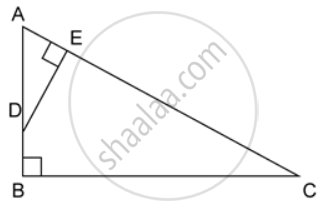
If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
In figure ABC and DBC are two triangles on the same base BC. Prove that
`"Area (ΔABC)"/"Area (ΔDBC)" = "AO"/"DO"`.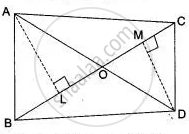
Two isosceles triangle have equal vertical angles and their areas are in the ratio of 36 : 25. Find the ratio between their corresponding heights.
In the adjoining figure ABC is a right angle triangle with ∠BAC = 90°, and AD ⊥ BC.
(i) Prove ΔADB ∼ ΔCDA.
(ii) If BD = 18 cm, CD = 8 cm find AD.
(iii) Find the ratio of the area of ΔADB is to area of ΔCDA.
