Advertisements
Advertisements
Question
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that :
- ΔAPB is similar to ΔCPD.
- PA × PD = PB × PC.
Solution
In trapezium ABCD
AB || DC
Diagonals AC and BD intersect each other at P.
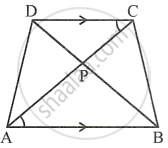
To prove:
- ΔAPB ∼ ΔCPD.
- PA × PD = PB × PC.
Proof: In ΔAPB and ΔCPD
∠APB = ∠CPD ...(Vertically opposite angles)
∠PAB = ∠PCD ...(Alternate angles)
∴ ΔAPB ∼ ΔCPD ...(AA axiom)
∴ `(PA)/(PC) = (PB)/(PD)`
`\implies` PA × PD = PB × PC
Hence proved.
APPEARS IN
RELATED QUESTIONS
State, true or false:
Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
In quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE : EC = BE : ED. Show that: ABCD is a trapezium.
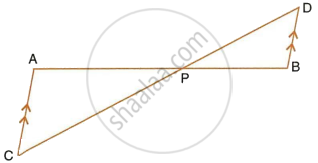
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that: ΔAPC and ΔBPD are similar.
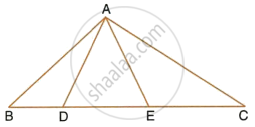
In the given figure, AD = AE and AD2 = BD × EC. Prove that: triangles ABD and CAE are similar.
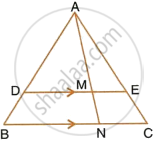
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.
- Write all possible pairs of similar triangles.
- Find lengths of ME and DM.
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
In the following figure, AB, CD and EF are perpendicular to the straight line BDF.
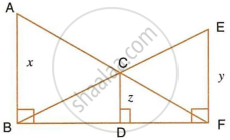
If AB = x and CD = z unit and EF = y unit, prove that : `1/x + 1/y = 1/z`
Triangle ABC is similar to triangle PQR. If AD and PM are altitudes of the two triangles, prove that : `(AB)/(PQ) = (AD)/(PM)`.
In the given figure, AB and DE are perpendiculars to BC.
Prove that : ΔABC ~ ΔDEC
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEf) = 64 cm2 and DE = 6.2 cm, find AB.
