Advertisements
Advertisements
Question
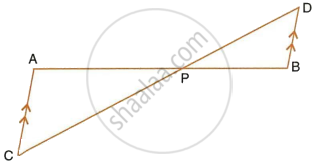
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that: If BD = 2.4 cm, AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm; find the lengths of PA and PC.
Solution
In ΔAPC and ΔBPD,
∠APC = ∠BPD ...(Vertically opposite angles)
∠ACP = ∠BDP ...(Alternate angles since AC || BD)
∴ ΔAPC ∼ ΔBPD ...(AA criterion for similarity)
So, `(PA)/(PB) = (PC)/(PD) = (AC)/(BD)`
`=> (PA)/(3.2) = (PC)/4 = 3.6/2.4`
So, `(PA)/(3.2) = (3.6)/(2.4)` and `(PC)/4 = (3.6)/(2.4)`
`=> PA = (3.6 xx 3.2)/2.4 = 4.8 cm`
And PC = `(3.6 xx 4)/(2.4)` = 6 cm
Hence, PA = 4.8 cm and PC = 6 cm
APPEARS IN
RELATED QUESTIONS
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that: DL : DP = AL : DC.
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm. Find lengths of ME and DM.
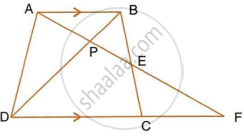
In the following figure, ABCD to a trapezium with AB ‖ DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm, Calculate: PE
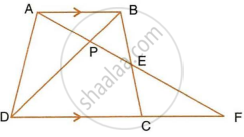
In the following figure, ABCD to a trapezium with AB || DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm, Calculate: AF
In the given figure, AB and DE are perpendiculars to BC.
If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
Two isosceles triangle have equal vertical angles and their areas are in the ratio of 36 : 25. Find the ratio between their corresponding heights.
In the adjoining figure ABC is a right angle triangle with ∠BAC = 90°, and AD ⊥ BC.
(i) Prove ΔADB ∼ ΔCDA.
(ii) If BD = 18 cm, CD = 8 cm find AD.
(iii) Find the ratio of the area of ΔADB is to area of ΔCDA.
On a map drawn to a scale of 1 : 2,50,000; a triangular plot of land has the following measurements : AB = 3 cm, BC = 4 cm and angle ABC = 90°.
Calculate:
- the actual lengths of AB and BC in km.
- the area of the plot in sq. km.
In the figure below, PB and QA are perpendiculars to the line segment AB. If PO = 6 cm, QO = 9 cm and the area of ΔPOB = 120 cm2, find the area of ΔQOA.
