Advertisements
Advertisements
Question
Two isosceles triangle have equal vertical angles and their areas are in the ratio of 36 : 25. Find the ratio between their corresponding heights.
Solution
ΔABC and ΔPQR be the two isosceles triangles such that
∠A = ∠P.
Then ΔABC ∼ ΔPQR.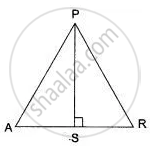
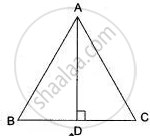
Let AD and PS be their height then
`"area (ΔABC)"/"area (ΔPQR)" = "AD"^2/"PS"^2`
⇒ `(36)/(25) = "AD"^2/"PS"^2`
⇒ `"AD"/"PS" = (6)/(5)`
⇒ AD : PS = 6 : 5.
APPEARS IN
RELATED QUESTIONS
State, true or false:
The diagonals of a trapezium divide each other into proportional segments.
In quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE : EC = BE : ED. Show that: ABCD is a trapezium.
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that: If BD = 2.4 cm, AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm; find the lengths of PA and PC.
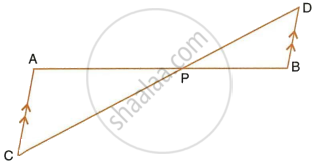
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that: DP : PL = DC : BL.
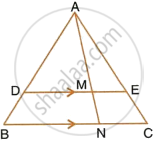
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.
- Write all possible pairs of similar triangles.
- Find lengths of ME and DM.
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.
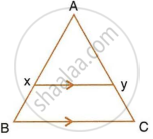
Find :
- `(AY)/(YC)`
- `(YC)/(AC)`
- XY
In the figure given below, AB || EF || CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm.
Calculate :
- EF
- AC
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
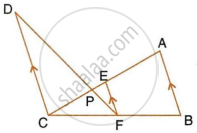
In the given figure ABC is a triangle with ∠EDB = ∠ACB.
(i) Prove that ΔABC ∼ ΔEBD.
(ii) If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of ΔBED = 9 cm2. Calculate the length of AB and area of ΔABC.
Triangles ABC and DEF are similar.
If AC = 19 cm and DF = 8 cm, find the ratio between the areas of two triangles.
