Advertisements
Advertisements
Question
In the given figure ABC is a triangle with ∠EDB = ∠ACB.
(i) Prove that ΔABC ∼ ΔEBD.
(ii) If BE = 6 cm, EC = 4 cm, BD = 5 cm and area of ΔBED = 9 cm2. Calculate the length of AB and area of ΔABC.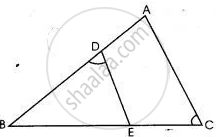
Solution
(i) In ΔABC and ΔEBD,
∠ACB = ∠EDB ...(given)
∠ABC = ∠EBD ...(common)
∴ ΔABC ∼ ΔEBD
Hence Proved.
(ii) We have, `"AB"/"BE"= "BC"/"BD"`
⇒ AB = `(6 xx 10)/(5) = 12 "cm"`.
(iii) `"Area of ΔABC"/"Area of ΔBED" = ("AB"/"BE")^2`
Area of ΔABC = `(12/16)^2 xx 9 "cm"^2`
= 4 x 9 cm2
= 36 cm2.
APPEARS IN
RELATED QUESTIONS
State, true or false:
Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
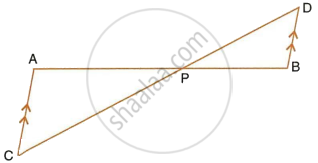
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that: ΔAPC and ΔBPD are similar.
In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that: OA × OD = OB × OC.
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that: AB × BC = BP × CA
Triangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and bisector of angle QPR meets QR at point M, prove that : `(AB)/(PQ) = (AD)/(PM)`.
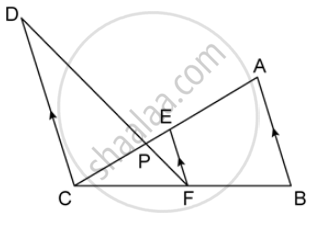
In the figure given below, AB ‖ EF ‖ CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm. Calculate : AC
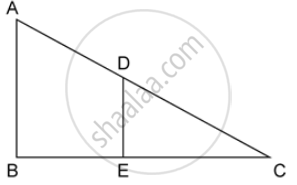
In the given figure, AB and DE are perpendiculars to BC.
Prove that : ΔABC ~ ΔDEC
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
Triangles ABC and DEF are similar.
If area (ΔABC) = 9 cm2, area (ΔDEF) = 64 cm2 and BC = 5·1 cm find AB.
Triangles ABC and DEF are similar.
If AC = 19 cm and DF = 8 cm, find the ratio between the areas of two triangles.
