Advertisements
Advertisements
Question
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that: AB × BC = BP × CA
Solution
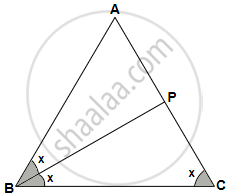
Consider ΔABC and ΔAPB
∠ABC = ∠APB ...[Exterior angle property]
∠BCP = ∠ABP ...[Given]
∴ ΔABC ∼ ΔAPB ...[AA criterion for similarity]
`(CA)/(AB) = (BC)/(BP)` ...(Corresponding sides of similar triangles are proportional)
`=>` AB × BC = BP × CA
APPEARS IN
RELATED QUESTIONS
State, true or false:
Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
Angle BAC of triangle ABC is obtuse and AB = AC. P is a point in BC such that PC = 12 cm. PQ and PR are perpendiculars to sides AB and AC respectively. If PQ = 15 cm and PR = 9 cm; find the length of PB.
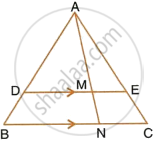
In the given figure, DE || BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.
- Write all possible pairs of similar triangles.
- Find lengths of ME and DM.
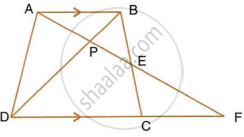
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
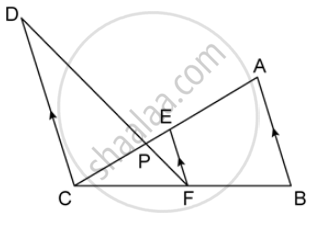
In the following figure, ABCD to a trapezium with AB ‖ DC. If AB = 9 cm, DC = 18 cm, CF = 13.5 cm, AP = 6 cm and BE = 15 cm, Calculate: PE
In the figure given below, AB ‖ EF ‖ CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm. Calculate : AC
Triangles ABC and DEF are similar.
If area (ΔABC) = 16 cm, area (ΔDEF) = 25 cm2 and BC = 2.3 cm find EF.
In the adjoining figure, ΔACB ∼ ∆APQ. If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm and AP = 2.8 cm find the area (∆ACB) : area (∆APQ).
In ΔABC, and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.
Triangles ABC and DEF are similar.
If area (ΔABC) = 16 cm2, area (ΔDEF) = 25 cm2 and BC = 2·3 cm find EF.
