Advertisements
Advertisements
Question
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that: CB : BA = CP : PA
Solution
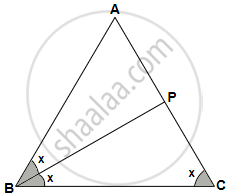
In ΔABC,
∠ABC = 2∠ACB
Let ∠ACB = x
`=>` ∠ABC = 2∠ACB = 2x
Given BP is bisector of ∠ABC
Hence ∠ABP = ∠PBC = x
Using the angle bisector theorem,
That is the bisector of an angle divides the side opposite to it in the ratio of other two sides.
Hence, CB : BA = CP : PA.
APPEARS IN
RELATED QUESTIONS
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
In the given figure, AB and DE are perpendiculars to BC.
Find the ratio of the area of a ΔABC : area of ΔDEC.

ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :

ΔADE ~ ΔACB.
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
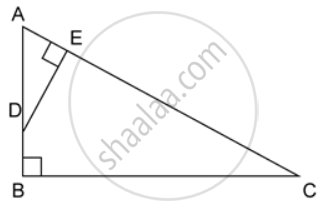
If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
Triangles ABC and DEF are similar.
If area (ΔABC) = 16 cm, area (ΔDEF) = 25 cm2 and BC = 2.3 cm find EF.
Triangles ABC and DEF are similar.
If AC = 19 cm and DF = 8 cm, find the ratio between the area of two triangles.
Triangles ABC and DEF are similar.
If area (ΔABC) = 36 cm2, area (ΔDEF) = 64 cm2 and DE = 6.2 cm, find AB.
In figure ABC and DBC are two triangles on the same base BC. Prove that
`"Area (ΔABC)"/"Area (ΔDBC)" = "AO"/"DO"`.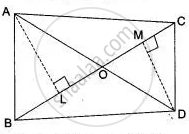
In the figure below, PB and QA are perpendiculars to the line segment AB. If PO = 6 cm, QO = 9 cm and the area of ΔPOB = 120 cm2, find the area of ΔQOA.
Triangles ABC and DEF are similar.
If AC = 19 cm and DF = 8 cm, find the ratio between the areas of two triangles.
