Advertisements
Advertisements
Question
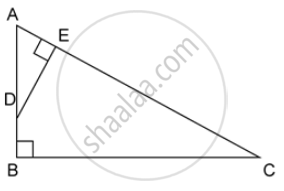
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
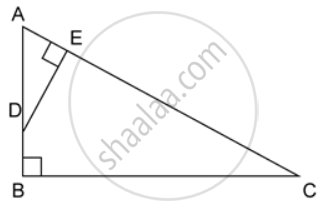
If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
Solution
Since ΔADE ~ ΔACB, their sides are proportional
`=> (AE)/(AB) = (AD)/(AC) = (DE)/(BC)` ....(1)
In ΔABC, by Pythagoras Theorem, we have
`AB^2 + BC^2 = AC^2`
`=> AB^2 + 5^2 = 13^2`
`=> AB = 12 cm`
From equation 1 we have
`4/12 = (AD)/13 = (DE)/5`
`=> 52/12= (AD)`
`=> AD = 4 1/3cm`
Also `4/12 = (DE)/5`
`=> DE = 20/12 = 5/3 = 1 2/3 cm`
APPEARS IN
RELATED QUESTIONS
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that: DP : PL = DC : BL.
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that: DL : DP = AL : DC.
In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that: ΔAOB is similar to ΔCOD.
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that: CB : BA = CP : PA
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E. Prove that: EL = 2BL.
In the following figure, AB, CD and EF are perpendicular to the straight line BDF.
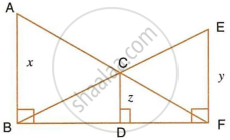
If AB = x and CD = z unit and EF = y unit, prove that : `1/x + 1/y = 1/z`
In the figure given below, AB || EF || CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm.
Calculate :
- EF
- AC
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
Find, area of ΔADE : area of quadrilateral BCED.
Triangles ABC and DEF are similar.
If AC = 19 cm and DF = 8 cm, find the ratio between the area of two triangles.
In the adjoining figure, ΔACB ∼ ∆APQ. If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm and AP = 2.8 cm find the area (∆ACB) : area (∆APQ).