Advertisements
Advertisements
Question
Triangles ABC and DEF are similar.
If area (ΔABC) = 16 cm, area (ΔDEF) = 25 cm2 and BC = 2.3 cm find EF.
Solution
We have
area (ΔABC) = 16cm2
area (ΔDEF) = 25 cm2
and BC = 2.3 cm
Since, `"area (ΔABC)"/"area (ΔDEF)" = "BC"^2/"EF"^2`
⇒ `(16)/(25) = (2.3)^2/"EF"^2`
⇒ `(2.3)/"EF" = (4)/(5)`
⇒ 4 EF = 5 x 2.3
⇒ EF = `(11.5)/(4)`
⇒ EF = 2.875 cm.
APPEARS IN
RELATED QUESTIONS
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that :
- ΔAPB is similar to ΔCPD.
- PA × PD = PB × PC.
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that: DL : DP = AL : DC.
In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that: ΔAOB is similar to ΔCOD.
In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that: OA × OD = OB × OC.
In ΔABC; BM ⊥ AC and CN ⊥ AB; show that:
`(AB)/(AC) = (BM)/(CN) = (AM)/(AN)`
In the following figure, AB, CD and EF are perpendicular to the straight line BDF.
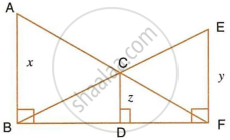
If AB = x and CD = z unit and EF = y unit, prove that : `1/x + 1/y = 1/z`
Triangle ABC is similar to triangle PQR. If AD and PM are corresponding medians of the two triangles, prove that : `("AB")/("PQ") = ("AD")/("PM")`.
In the following figure, ∠AXY = ∠AYX. If `(BX)/(AX) = (CY)/(AY)`, show that triangle ABC is isosceles.
In the given figure, AB and DE are perpendiculars to BC.
Prove that : ΔABC ~ ΔDEC
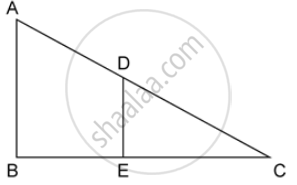
In the given figure, AB and DE are perpendiculars to BC.
If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.