Advertisements
Advertisements
Question
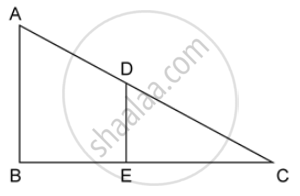
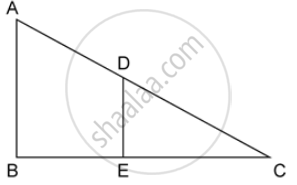
In the given figure, AB and DE are perpendiculars to BC.
If AB = 6 cm, DE = 4 cm and AC = 15 cm. Calculate CD.
Solution
In ΔABC and ΔDEC,
∠ABC = ∠DEC ...(both are right angles)
∠ACB = ∠DCE ....(common angles)
ΔABC ∼ ΔDEC ...(AA criterion for similarity)
`=> (AB)/(DE) = (AC)/(CD)`
`=> 6/4 = 15/(CD)`
`=>` CD = 10 cm
APPEARS IN
RELATED QUESTIONS
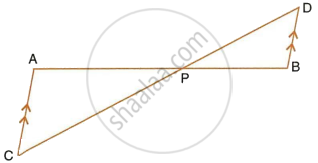
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that: ΔAPC and ΔBPD are similar.
In the given figure, AB || DC, BO = 6 cm and DQ = 8 cm; find: BP × DO.

In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that: CB : BA = CP : PA
In the following figure, XY is parallel to BC, AX = 9 cm, XB = 4.5 cm and BC = 18 cm.
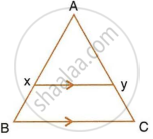
Find :
- `(AY)/(YC)`
- `(YC)/(AC)`
- XY
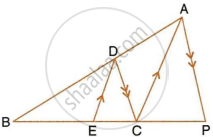
In the following figure, DE || AC and DC || AP. Prove that : `(BE)/(EC) = (BC)/(CP)`.
In the figure given below, AB ‖ EF ‖ CD. If AB = 22.5 cm, EP = 7.5 cm, PC = 15 cm and DC = 27 cm. Calculate : AC
In the given figure, AB and DE are perpendiculars to BC.
Prove that : ΔABC ~ ΔDEC
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
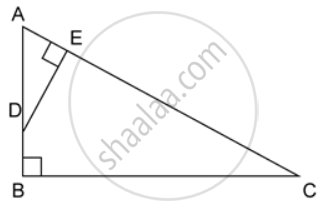
If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
Triangles ABC and DEF are similar.
If area (ΔABC) = 9 cm2, area (ΔDEF) = 64 cm2 and BC = 5·1 cm find AB.
Triangles ABC and DEF are similar.
If AC = 19 cm and DF = 8 cm, find the ratio between the areas of two triangles.
