Advertisements
Advertisements
Question
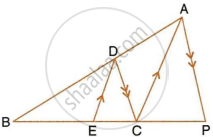
In the following figure, DE || AC and DC || AP. Prove that : `(BE)/(EC) = (BC)/(CP)`.
Solution
In the given figure,
DE || AC and DC || AP
To prove: `(BE)/(EC) = (BC)/(CP)`
Proof: In ΔBCA, we have
ED || CA
Since a line drawn is || to one side of a Δ divides the other two side proportionality.
∴ `(BE)/(EC) = (BD)/(DA)` ...(i)
Similarly in ΔBPA; we have DC || AP
Since a line drawn is || to one side of a Δ divides the other two side proportionality.
∴ `(BC)/(CP) = (BD)/(DA)` ...(ii)
From (i) and (ii),
`(BE)/(EC) = (BC)/(CP)`
Hence proved.
APPEARS IN
RELATED QUESTIONS
In quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE : EC = BE : ED. Show that: ABCD is a trapezium.
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that: DL : DP = AL : DC.
In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that: ΔAOB is similar to ΔCOD.
In the given figure, AD = AE and AD2 = BD × EC. Prove that: triangles ABD and CAE are similar.
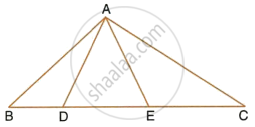
In the given figure, AB and DE are perpendiculars to BC.
Prove that : ΔABC ~ ΔDEC
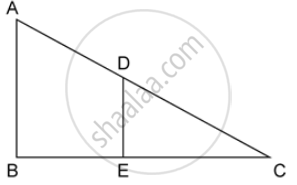
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :

ΔADE ~ ΔACB.
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that :
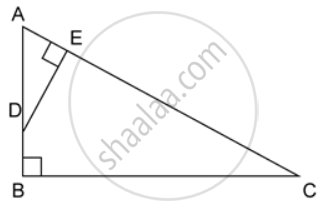
If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
In the adjoining figure, ΔACB ∼ ∆APQ. If BC = 10 cm, PQ = 5 cm, BA = 6.5 cm and AP = 2.8 cm find the area (∆ACB) : area (∆APQ).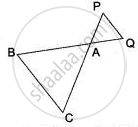
In ΔABC, and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ΔADE and ΔABC.
Triangles ABC and DEF are similar.
If area (ΔABC) = 16 cm2, area (ΔDEF) = 25 cm2 and BC = 2·3 cm find EF.
