Advertisements
Advertisements
Question
In the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm. L is a point on PR such that RL : LP = 2 : 3. QL produced meets RS at M and PS produced at N.

Find the lengths of PN and RM.
Solution
In ∆RLQ and ∆PLN,
∠RLQ = ∠PLN ...(Vertically opposite angles)
∠LRQ = ∠LPN ...(Alternate angles)
∆RLQ ~ ∆PLN ...(AA Similarity)
∴ `(RL)/(LP) = (RQ)/(PN)`
`2/3 = (10)/(PN)`
PN = 15 cm
In ∆RLM and ∆PLQ
∠RLM = ∠PLQ ...(Vertically opposite angles)
∠LRM= ∠LPQ ...(Alternate angles)
∆RLM ~ ∆PLQ ...(AA Similarity)
∴ `(RM)/(PQ) = (RL)/(LP)`
`(RM)/16 = 2/3`
`RM = 32/3 = 10 2/3 cm`
APPEARS IN
RELATED QUESTIONS
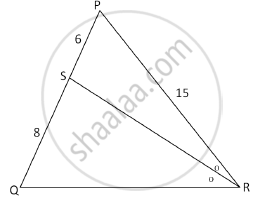
In the following figure, in ΔPQR, seg RS is the bisector of ∠PRQ. If PS = 6, SQ = 8, PR = 15, find QR.
In the given figure ΔABC and ΔAMP are right angled at B and M respectively. Given AC = 10 cm, AP = 15 cm and PM = 12 cm.

1) Prove ΔABC ~ ΔAMP
2) Find AB and BC.
In ΔABC, D and E are the points on sides AB and AC respectively. Find whether DE || BC, if:
- AB = 9 cm, AD = 4 cm, AE = 6 cm and EC = 7.5 cm.
- AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and AE = 1.6 cm.
In the adjoining figure. BC is parallel to DE, area of ΔABC = 25 sq cm, area of trapezium BCED = 24 sq cm, DE = 14 cm. Calculate the length of BC.
In ΔABC, D and E are the mid-point on AB and AC such that DE || BC.
If AD = 8cm, AB = 12cm and AE = 12cm, find CE.
ABCD is a parallelogram whose sides AB and BC are 18cm and 12cm respectively. G is a point on AC such that CG : GA = 3 : 5 BG is produced to meet CD at Q and AD produced at P. Prove that ΔCGB ∼ ΔAGP. Hence, fi AP.
Two figures are similar. If the ratio of their perimeters is 8:16. What will be the ratio of the corresponding sides?
A model of cargo tuck is made to a scale of 1:40. The length of the model is 15cm. Calculate: The length of the truck
ΔABP ~ ΔDEF and A(ΔABP) : A(ΔDEF) = 144:81, then AB : DE = ?
∆ABC ~ ∆PQR. If AM and PN are altitudes of ΔABC and ∆PQR respectively and AB2 : PQ2 = 4 : 9, then AM : PN = ______.
